
Probability is a flexible language for reasoning about our level of certainty
- Sampling
- Axioms
- Random Variable
- Joint probability
- Conditional Probability
- Independence
- Marginalization
- Bayse' theorem practice
- Expectation and Variables
1. Sampling
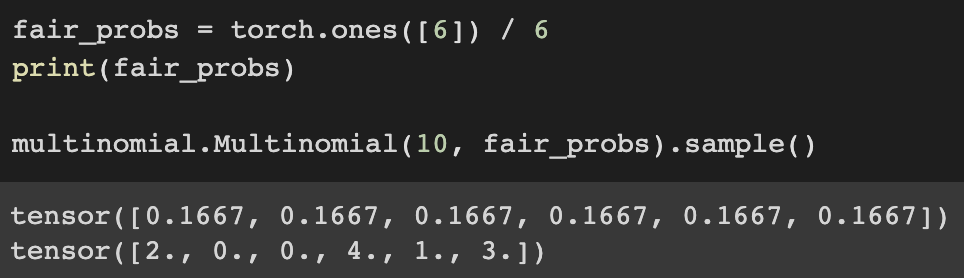
Correspond to the probs, we can randomly draw mulitple samples.

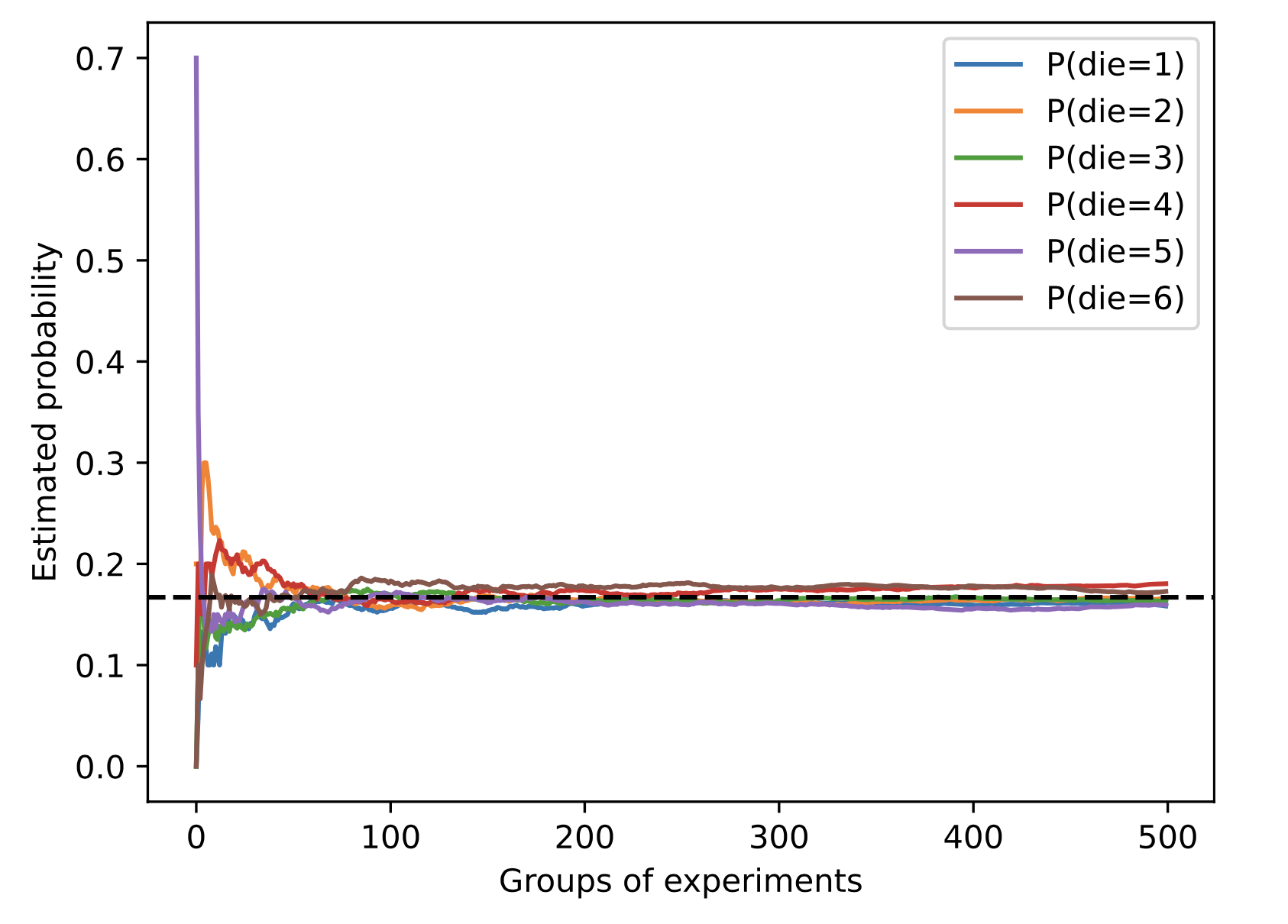
conduct 500 groups of experiments where each group draws 10 samples. (sampling)
2. Axioms
When dealing with rolls of a die,
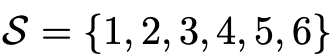
this is called sample space (or outcome space)
each element is an outcome.
An event is a set of outcomes from a given sample space. for instance “seeing an odd number"
3. Random Variable
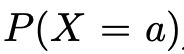
Random variable X which takes a.
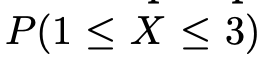
probability of X which takes from 1 to 3.
4. Joint probability
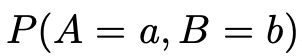
We call this joint probability A = a and B = b should happen simultaneously.
5. Conditional Probability
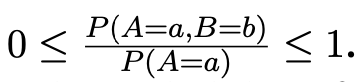
We call this conditional probability.
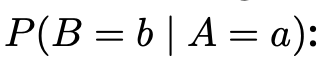
it is the probability of B=b, provided that A=a has occured.
using the definition of conditional theory we can derive Bayes' Theorem
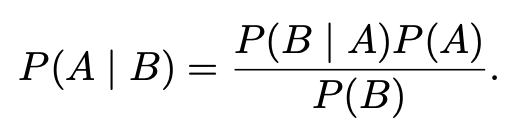
6. Independence
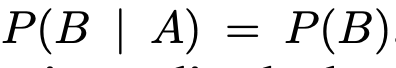
in this case above we call that A, B are independent, which means occurrence of one event of A does not reveal any information about the occurrence of an event of B.
We can express this like the image below.
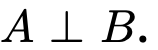
if their joint distribution is same with the product of their individual distributions.
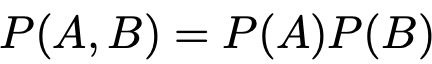
Two random variables are independent
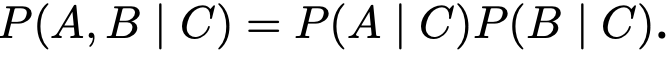
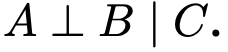
two random variables A and B are conditionally independent given another random variable C
7. Marginalization
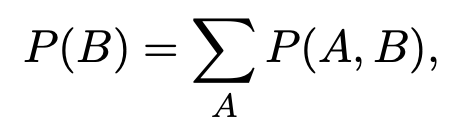
P(B) is same with P(A1, B) + P(A2, B) + ,..... P(An, B). we call this marginalization
8. Bayse' Theorem Practice
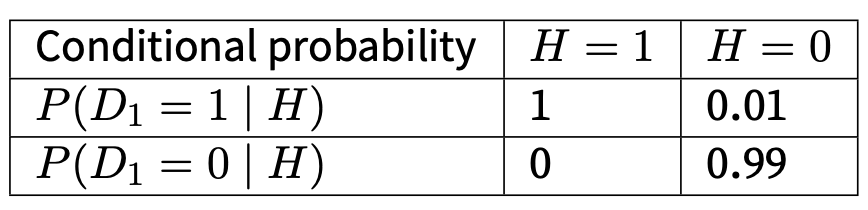
D denotes diagnous (1 is positive 0 is negaitve). H denotes HIV (1 positive, 0 negative)
Diagnouses are quite accurate because its probablitity of detecting positive even though the patients are healty is only 0.01.
But what is the probability of P(H = 1 | D = 1) (doctor said positive and it is really positive)
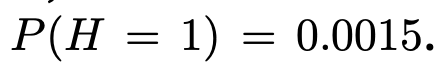
let's say P(H=1) is 0.0015
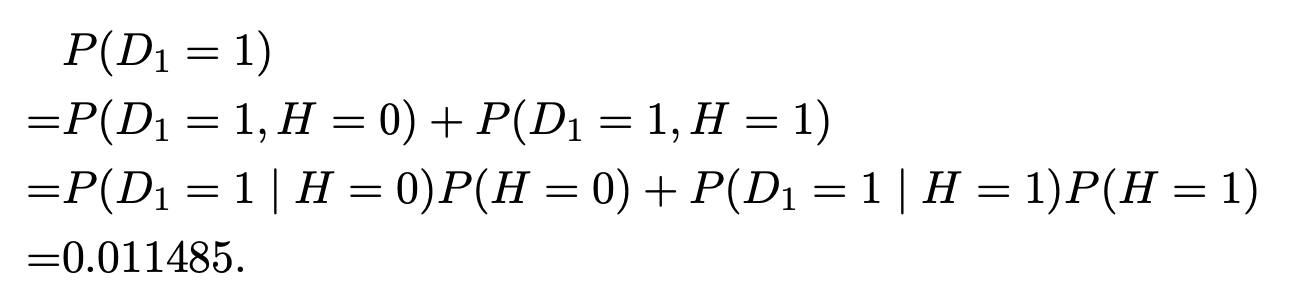
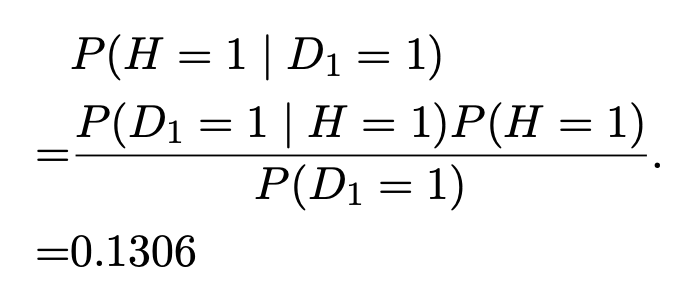
It is only 13%. which means that diagnouse is only corrent by 13%.
What if we add one more test to get clarity
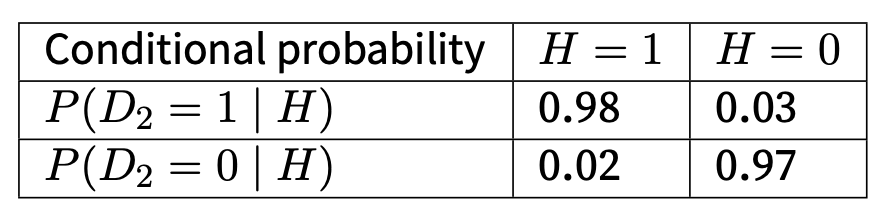
The second test is not good as the first one.
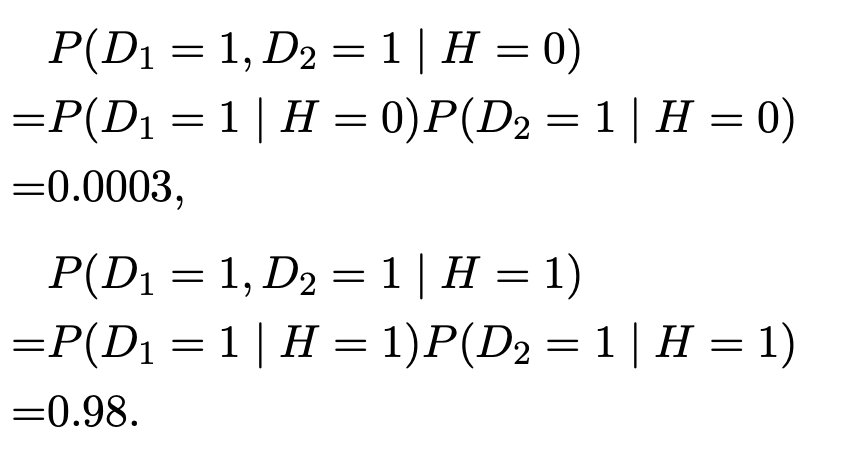
given H, D1 and D2 are conditionally independent.
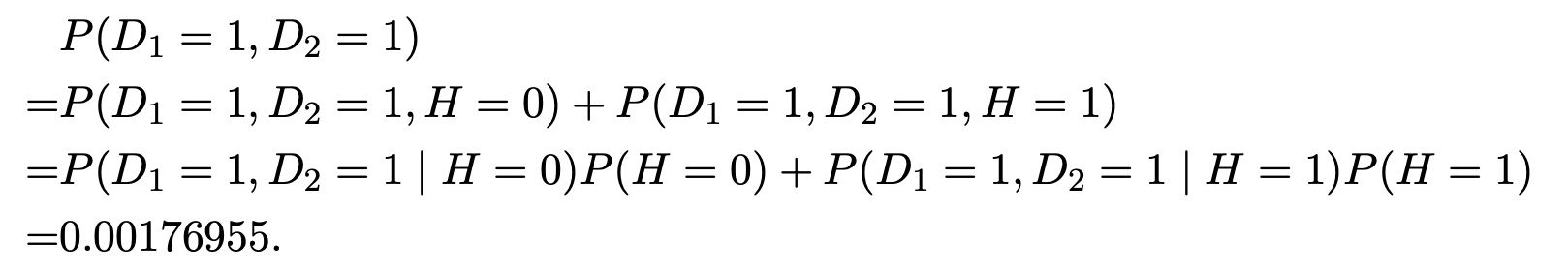
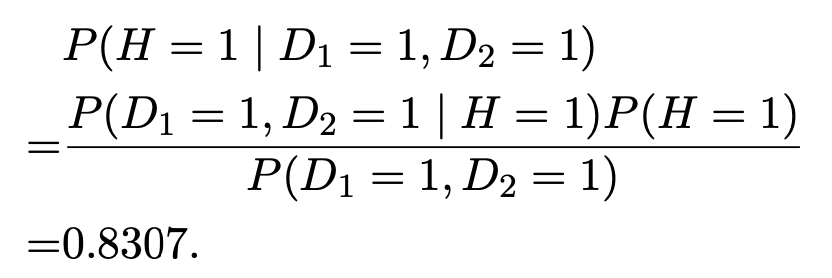
It shows that when both tests say positive, the probability of postivie HIV is 83 percent.
Even though the second test is less accurate than the first one, it improved the estimation.
9. Expectation and Variables
To summarize key characteristics of probability distributions, we need some measures. The expectation of the random variable X is denoted as

how much the random variable X deviates from its expectation. This can be quantified by the variance
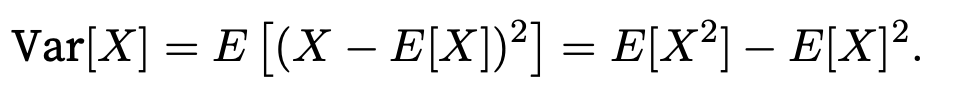
It's square root is called standard deviation.
'ComputerScience > Machine Learning' 카테고리의 다른 글
| Deep Learning - 2.2 Linear Regression Implementation from Scratch (0) | 2022.08.13 |
|---|---|
| Deep Learning - 2.1 Linear Regression (0) | 2022.08.11 |
| Deep Learning - 1.5 Automatic Differentiation (0) | 2022.08.06 |
| Deep Learning - 1.4 Calculus (0) | 2022.08.03 |
| Deep Learning - 1.3 Linear Algebra (0) | 2022.07.29 |



