
Deep learning frameworks can automate the calculation of derivatives.
- Simple Example
- Backward for Non-Scalar Variables
- Detaching Computation
- Gradient of python control flow
1. Simple Example
While backpropagation, deep learning framework automatically calcuate gradients.
first attach gradients to those variables with respect to which we desire partial derivatives.

In this example f = 2(x^2 + y^2 + z^2, ....). (scalar)
Gradient of f is [4x, 4y, 4z, .... ]
Gradient of f at [0,1,2,3] is [0,4,8,12]

In this example f = x + y + z + .... (scalar)
gradient of f is [1,1,1,.....]
Gradient of f at [0,0,0,0] is [0,4,8,12]

f = x * y + x
gradiet of f is [y+1, x]
gradient of f at [3,1] is [2,3]
2. Backward for Non-Scalar Variables
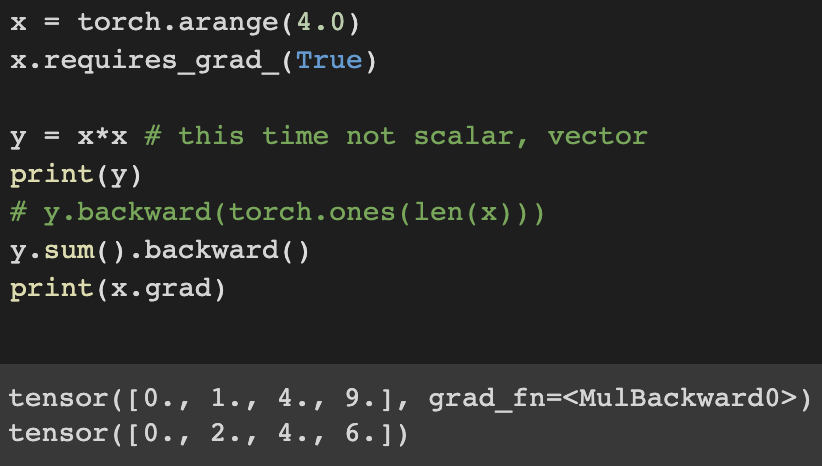
In this example y is not a scalar, it's vector. So to make y into scalar, we sum all the partial derivatives.
Then f = x^2 + y^2 + z^2, ..... (scalar)
Gradient of f is [2x, 2y, 2z, .... ]
Gradient of f at [0,1,2,3] is [0,2,4,6]
3. Detaching Computation

y = x * x / u = y / z = u * x
Gradient of z is [ u ]
u at [0,1,2,3] is [0,1,4,9]
Detatch y to return a new variable u, same as y but discards the info about how y was computed.
In other words, gradient will not backward u through x, just treat u as a constant (instead of partial derivative z = x*x*x)
4. Computing the Gradient of Python ControlFlow
even if building the computational graph of a function required passing through Python control flow (e.g., conditionals, loops, and arbitrary function calls), we can still calculate the gradient of the resulting variable.

'ComputerScience > Machine Learning' 카테고리의 다른 글
| Deep Learning - 2.1 Linear Regression (0) | 2022.08.11 |
|---|---|
| Deep Learning - 1.6 Probability (0) | 2022.08.09 |
| Deep Learning - 1.4 Calculus (0) | 2022.08.03 |
| Deep Learning - 1.3 Linear Algebra (0) | 2022.07.29 |
| Deep Learning - 1.2 Data Preprocessing (0) | 2022.07.28 |



