
Let's briefly review the subset of basic linear algebra.
- Scalars
- Vectors
- Matrices
- Tensors
- Reduction
- sum
- mean
- non-reduction sum
- cumulated sum
- Dot products
- Norms
1. scalars
Scalar variables are denoted by lowercase letters.
A scalar is represented by a tensor with just one element.

2. vectors
A vector is just an array of numbers. We usually denote vectors as bold-faced, lowercased letters. We work with vectors via one-dimensional tensors.
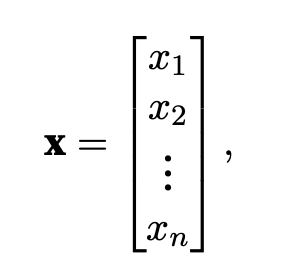
vector is represents as the image above, column vector is usually the defualt orientation of vector.

This means that vector x has n length. Length is commonly called the dimension of vector.
Vector is one dimention tensor so it's also available to get length through shape.
Not to confuse, dimensionality of tensor indicates the number of axis.
len() of a tensor always returns the number of elements of first axis.
3. Matrices


Matrices are denoted by bold-faced, capital letters. which are represented as tensors with twe axes.
Matrix A consist of m rows and n columns of real valued scalars

We can define matrix in terms of row vectors.


Transpose exchange matrix's columns and rows. if B = AT then bji = aij for any i and j.

If the number of rows and columns are same, we call it square matrix.
And. if A = A.T then A is called symmetric matrix

4. Tensors
Tensors describe n-dimentianal arrays with arbitrary number of axes.


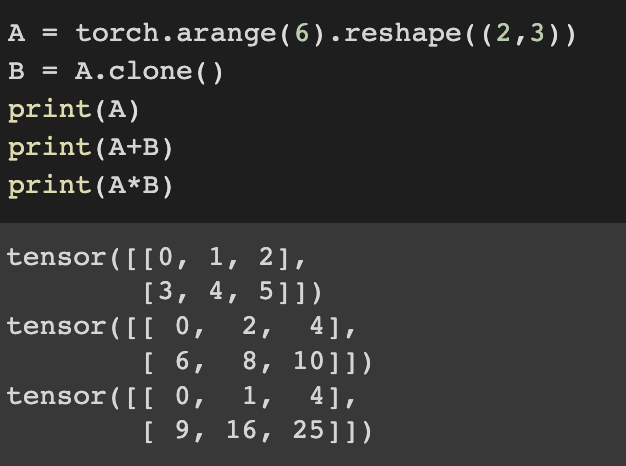
Elementwise operatoin is also availbe with tensor

Both matrices' size should be same.
We express elementwise tensor multiplication with math notation like above. It is called Hadamardproduct.

5. Reduction (sum, mean, non-reduction sum, cumulated sum)
Sum all elements of tensors

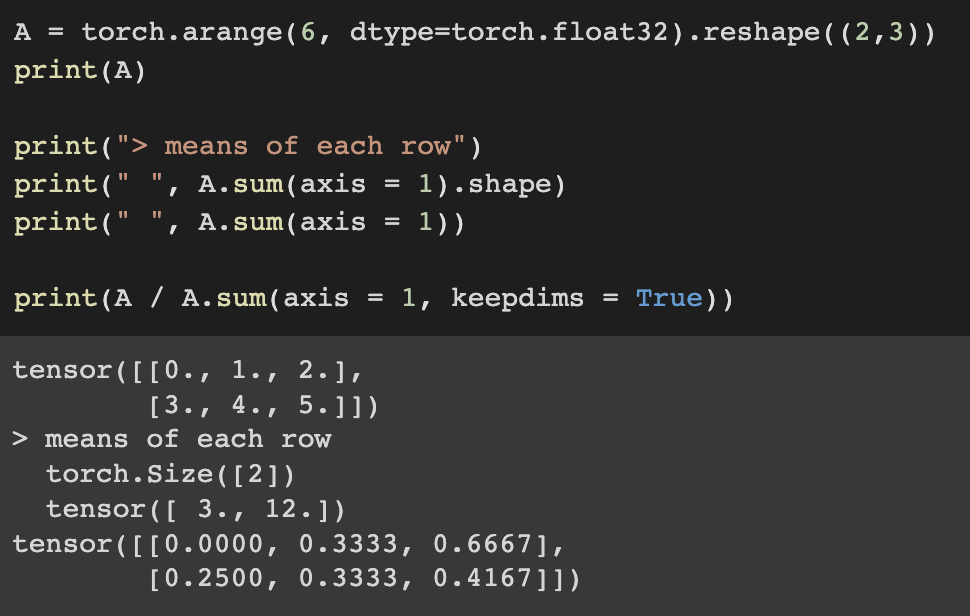
Reduce row axis by summing up elements of all the rows

Reduce colum axis by summing up elements of all the columns

Likewise, the function for calculating mean can also reduce a tensor along the specified axes.

While doing reduction sum(or mean), sometimes you may want to keep the number of axes.
For instance, you can divide each elements of rows(or columns) by reduction sum(or mean) with broadcasting.
You can also calcuate cumulated sum along specified axes, keeping tensor's shape.

6. Dot products (multiplicatoin)

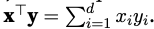
Given two vectors, their dot product can be deneoted like below
For vector cases, sum of elementwise multiplications is same as dot product.
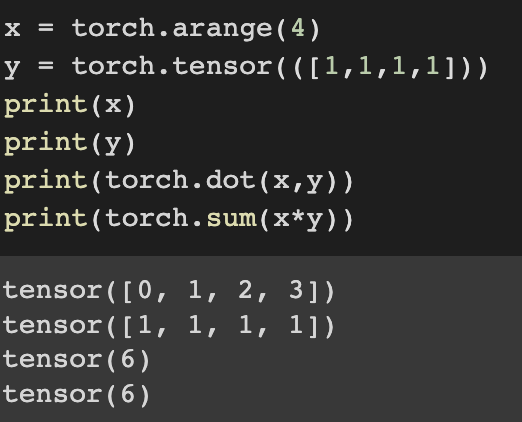
Now let's try matrix-vector product.
When we call torch.mv(A,x) with a Matrix A and a vector x, a matrix-vector dot product is performed.
A's length along axis 1 has to be same with the dimention of x.

What about Matix-Matrix Multiplication. It would be quite straightforward now.



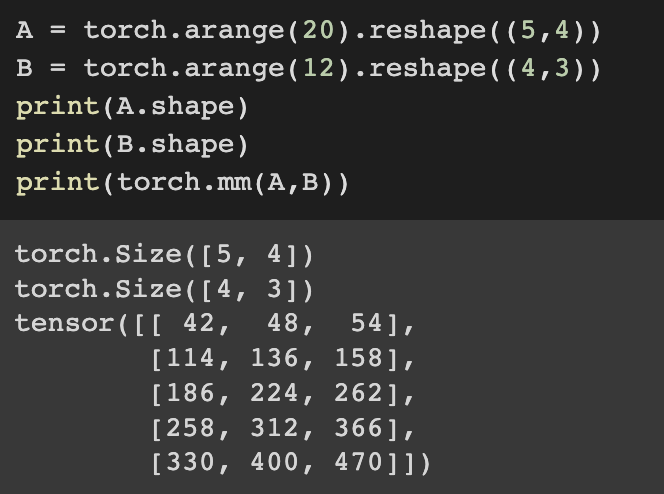
Simply by calling torch.mm(), matrix-matrix multiplication cam be performed.
7. Norms
Norm of a vector tells how big a vector is. It's similar with distance.
The most important components of deep learning algorithms, minimize the distance between pre-dictions and the ground-truth observations, are expressed as norm.

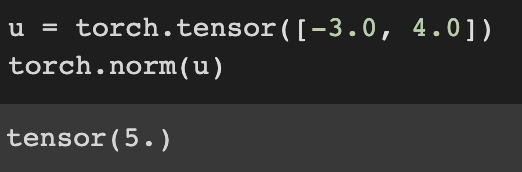
L2 Norm is the square root of the sum of the squares of vector elements. substripe 2 is often omitted in L2 norm.


In the same way, L1 Norm can be calculated like above, sum of the absolute values of the vector elements.
Lp norm:
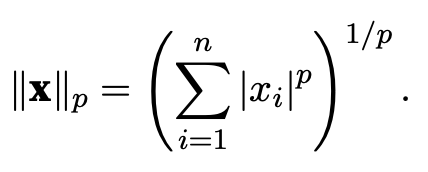
Frobenius norm of a Matrix X(mxn) is the square root of the sum of the squares of the matrix elements.


'ComputerScience > Machine Learning' 카테고리의 다른 글
| Deep Learning - 1.5 Automatic Differentiation (0) | 2022.08.06 |
|---|---|
| Deep Learning - 1.4 Calculus (0) | 2022.08.03 |
| Deep Learning - 1.2 Data Preprocessing (0) | 2022.07.28 |
| Deep Learning - 1.1 Data manipulation (0) | 2022.07.27 |
| AI - 13. Convolutional Neural Network (0) | 2021.12.10 |



