Factorization Machines
In this paper, we introduce Factorization Machines (FM) which are a new model class that combines the advantages of Support Vector Machines (SVM) with factorization models. Like SVMs, FMs are a general predictor working with any real valued feature vector.
ieeexplore.ieee.org
Factorization Machines(FM)은 support vector machine(SVM)과 factorization model의 장점을 합한 새로운 예측기이다.
1) sparse setting에서 parameter estimation이 가능하다 (unlike SVM)
1-1) sparse setting이 뭔가?
1-2) sparse setting에서 SVM이 왜 동작하지 않는가?
1-3) Factorization이 뭔가?
1-4) Factorization Model이 뭔가?
1-5) FM은 어떻게 sparse setting에서 잘 동작하는가?
2) linear complexity를 갖는다.
2-1) FM은 어떻게 학습시키는가?
2-2) d-way Factionzation Machine
3) general한 feature vector에 대해서 동작이 가능하다.
1-1) sparse setting이 뭔가?
실세계의 feature vector는 굉장히 sparse한 경우가 많다. feature vector의 대부분이 0을 차지하면서 차원은 굉장히 큰 경우를 말한다.

논문에서 예시로 든 feature vector의 모습이다. (유명한 factorization model에서 사용하던 input을 가져왔다고 한다.)
BLUE: 사용자, 1인 값은 한개만 존재한다.
RED: 지금 평가하려고 하는 영화
YELLOW: 이제까지 평가한 영화들과 점수 (합1로 normalize되어있다)
GREEN: Jan. 2009 이후 지난 달의 수
BROWN: 직전에 평가한 영화
TRAGET: User의 RED 영화에 대한 평가 점수
1-2) sparse setting에서 SVM이 왜 동작하지 않는가?
SVM은 vector space에 존재하는 점들을 구분하는 hyperline을 구해야하는데 각 점의 좌표에 해당하는 값들이 대부분 0인 경우는 의미 있는 파라미터를 학습하기 어렵다.
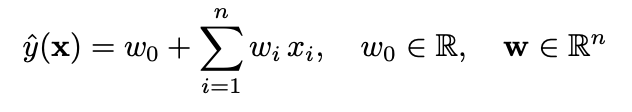
linear SVM의 모습이다. input data x = {사용자 one-hot encoding 벡터, 아이템 one-not encoding 벡터}라고 하자. 대부분 0이므로 굉장히 sparse 하다.
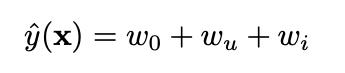
active user u, active item i 에 대해서 svm 모델의 식을 나타내면 위와 같다. 모델이 굉장히 심플하기 때문에 sparsity setting에서도 파라미터 추정이 가능하다.
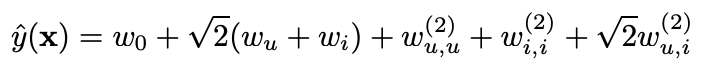
이번에는 Polynomial SVM의 경우를 생각해보자. 여기서 w_u는 w_u,u와 사실상 같은 것을 표현하므로 w_u,u, w_i,i를 생략할 수 있다. 그럼 w_u,i를 빼면 linear SVM과 같다. 그런데 w_u,i를 추론하는데 도움이 될 데이터는 사실상 많아야 한개가 training data에는 존재한다. 예를들면 (Alice, Titanic)은 한개 있고 (Alice Star Treck)은 아예 없다. 즉 최대 마진을 구하는 SVM의 경우 w_a, ST = 0이 된다. (A와 Star treck같의 interation이 없다.) 즉 SVM은 2-way interation을 전혀 예측에 활용하지 못한다. linear SVM보다 나을 것이 전혀 없다.
따라서 정리하면 굉장히 sparse한 환경에서는 (i,j)가 둘다 0이 아닌 데이터가 아주 적거나 거의 없기 때문에 parameter w_i,j 를 추정하기가 어렵다.
1-3) Factorization이 뭐야?
Matrix Factorization이라는 개념을 먼저 알고가자.
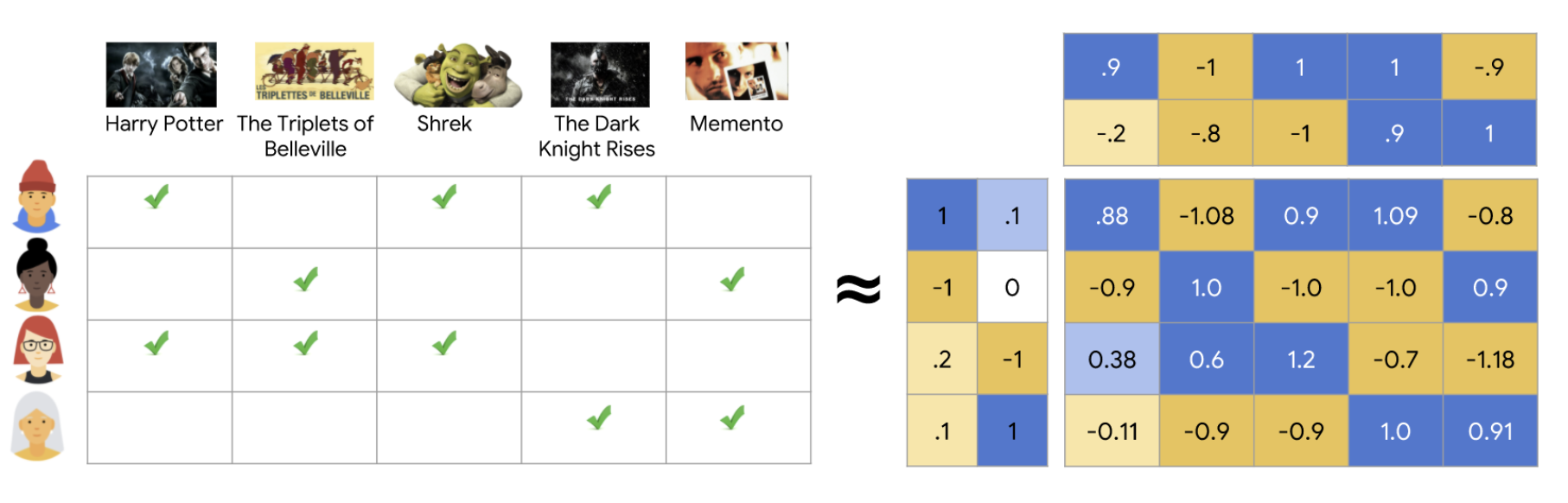
유저가 어떤 영화에 대해서 몇점의 평가를 내릴지 알면 추천시스템으로 활용할 수 있다. 대게 유저가 모든 영화에 대한 평가를 남길 수 없기 때문에 대부분 왼편의 rating matrix는 굉장히 sparse하다.
Matrix Factorization은 (user수 * f) * (f * item수)로 왼편의 행렬을 분해하는 것이다. 그러면 분해한 두 행렬로 왼편 sparse matrix의 빈칸을 채울 수 있다.
두 벡터를 user latent vector, item latent vector라고 부를 수 있다.
1-4) Factorization Model이 뭔가?
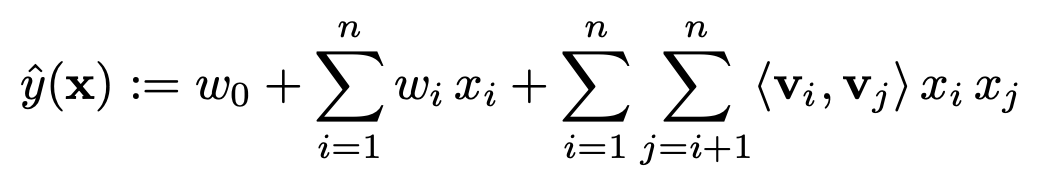
FM(degree=2)을 수식으로 표현하면 위와 같다.
w_0 : global bias이다.
x = [x_0, ... , x_i, ..., x_n] : feature vector x
w = [w_0, ..., w_i, ..., w_n] : weight w
w는 feature vector를 구성하는 개별 값들을 위한 가중치이다.
<V_i, V_j> : factorization parameter, 두 latent 벡터의 내적을 의미한다. w_i,j같은 파라미터를 두지 않고 x_i, x_j의 상호작용 계수를 factorization으로 계산한다. 이것이 sparse setting에서 high order interaction을 가능하게 만드는 key point이다.
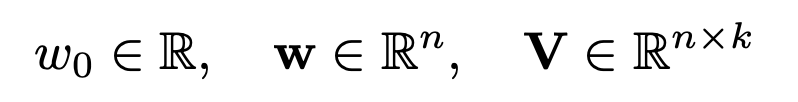
데이터를 통해 모델을 구성하는 위 세가지를 구해야한다. (k는 factorization의 차원을 결정하는 하이퍼파라미터이다)
1-5) FM은 어떻게 sparse setting에서 잘 동작하는가?

Alice(A)가 Star Trek(ST)를 예측한다고 가정해보자. 학습 데이터에는 당연히 xA 와 xST 가 0이 아닌 데이터가 없다. 그럼 두 변수 사이에 상관 관계는 다음과 같다. (wA,ST = 0) 하지만 factorized interation parameters <V_A, V_ST>는 다르다.
유저 B, C가 ST영화에 대해 평가한 데이터가 있으므로 V_ST가 학습될 것이고
유저 B, C가 유저 A와 공유하는 영화 SW를 평가한 데이터로부터 V_A가 학습될 것이다.
즉 정리하면 A와 ST의 관계를 나타내는 데이터는 없지만 다른 데이터들의 interaction을 통해 V_A, V_ST가 학습되고 결국은 A의 ST에 대한 평가를 알 수 있게 된다.
이것이 바로 하나의 interaction을 나타내는 데이터가 다른 관련된 interaction parameter를 추정하는데 도움을 주는 것이다.
따라서 굉장히 sparse setting에서도 충분하지 않은 데이터로 interactions between parameters를 추정할 수 있다.
input을 구성하는 데이터에 계속해서 새로운 feature들을 나열할 수 있다. FM은 이 모든 column들간의 interaction을 모델링 할 수 있다. (A, B간의 interaction 혹은 A, Time간의 interaction 등) 즉 user, item 뿐만 아니라 다양한 context정보들도 모델의 feature로 활용할 수 있어 훨씬 general하게 사용이 가능하다.
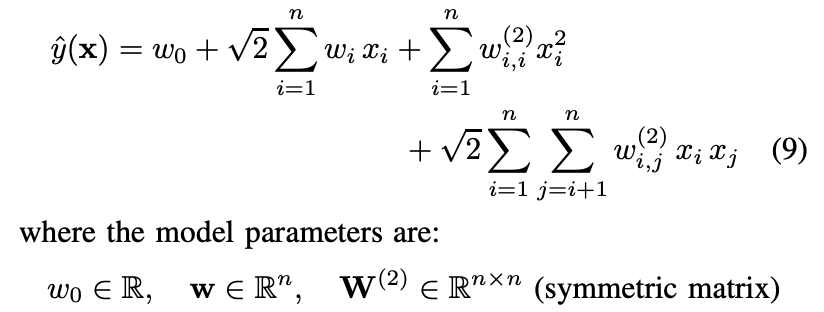
polynomial SVM 모델이다. FM처럼 svm도 high-order interaction을 잡을 수 있지만 보면 w_i,j는 i와 j의 interaction parameter인데 w_i,j와 w_i,l은 완전히 독립적이다.
하지만 FM의 경우 <vi, vj> 와 <vi, vl>은 서로 shared parameter로 인해 의존적이다. 이것을 바로 factorized라고 한다.
2) linear complexity를 갖는다.
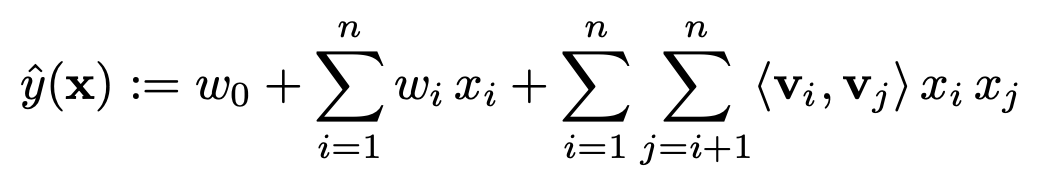
이 식을 그대로 사용하여 y(x)를 구하려면 O(n * n * k) 가 걸린다. (degree=2의 경우) 하지만 식을 reformulate를 해보자.
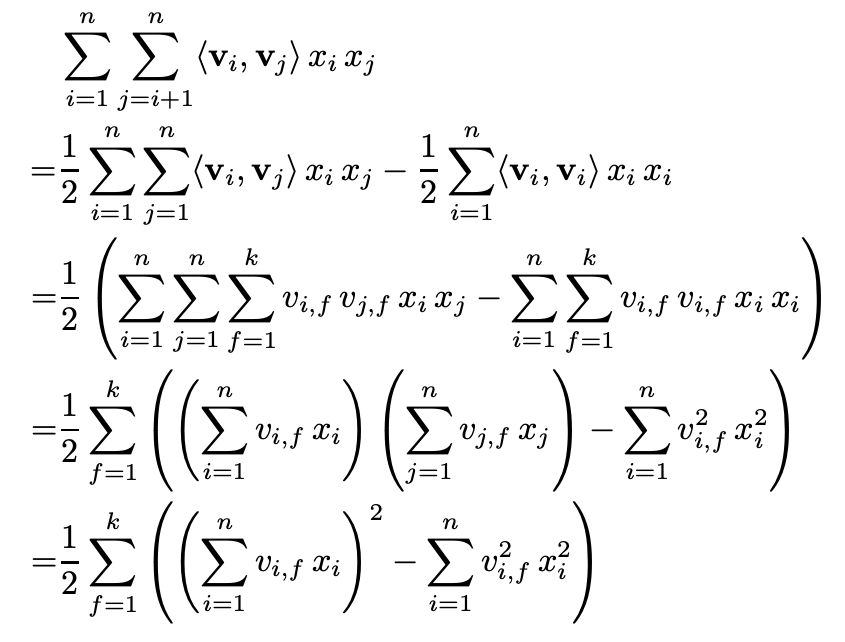
맨 아래 도출식을 보면 O(k * n)으로 구할 수 있다. (degree=2의 경우) sparse setting에서는 0이 대부분이므로 O(k * 0이 아닌 값들의 평균 갯수)로 더 줄어든다.
2-1) FM은 어떻게 학습시키는가?
다양한 Loss를 적용해서 SGD를 통해 FM의 파라미터를 학습시킬 수 있다.
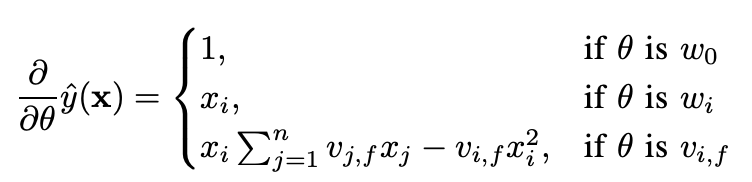
2-2) d-way Factionzation Machine
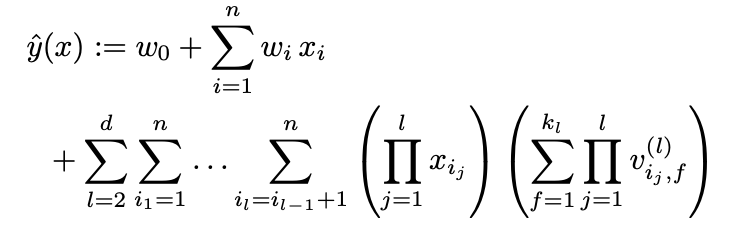
이 식으로만 보면 O(k_d * n^d) 이지만 마찬가지로 reformulating을 하면 linear time으로 줄일 수 있다.
이런식으로 input vector x를 구성하는 모든 feature들의 interaction을 모델링할 수 있다.
full parametrized 방식보다 이렇게 factorized interaction를 사용해서 모든 가능한 Interaction을 모델링하는 이유가 있다.
이렇게 함으로써 high sparsity setting에서 더 interaction들을 잘 추정할 수 있고 그에 따라 관찰되지 않은 interaction들도 추정할 수 있게 된다. 또한 prediction과 Learning이 모두 Linear time에 이루어진다. 이 점이 다양한 loss에 대해 SGD를 사용한 최적화를 가능하게 한다.
3) general한 feature vector에 대해서 동작이 가능하다.
Factorization Model들과 FM을 비교해보면 알 수 있다.
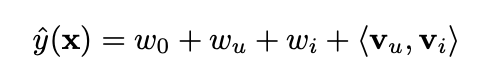
u=1, i=1인 항만 남기고 0인 항을 전부 drop하면 위의 식이 나오는데 이는 PARAFAC을 포함하는 모양이며
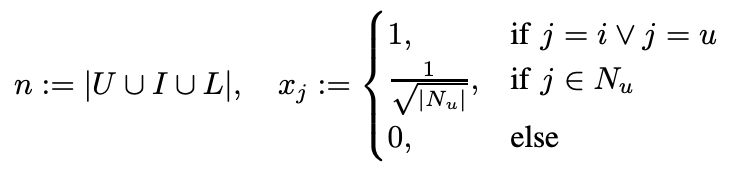
SVD++가 사용하는 input x를 FM(d=2)에 넣어보면
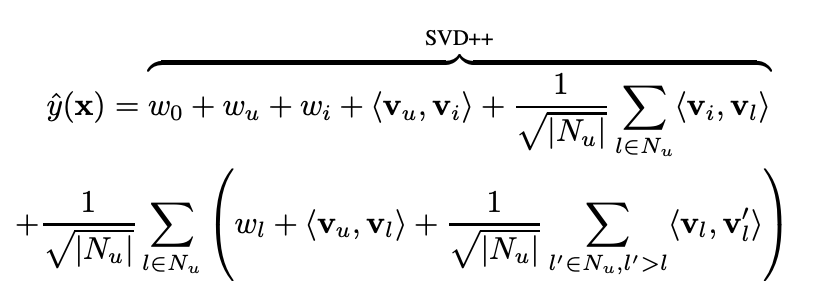
이렇게 나오는데 정확히 SVD++ 모델을 포함한다. 게다가 추가로 user와 N_u의 pair끼리의 interaction, N_u를 구성하는 feature들끼리의 interaction도 고려하는 모양이다.
심지어 이전 구매 품목을 기반으로해서 사용자에게 product rank를 추천해주는 Factorized Personalized Markov Chain(FPMC) 또한 FM이 모방할 수 있음을 보인다.
이렇듯 FM은 어떤 input형식에도 구애받지 않으면서 sota 모델들을 mimic할 수 있다.



