Neural RRT*: Learning-Based Optimal Path Planning
Rapidly random-exploring tree (RRT) and its variants are very popular due to their ability to quickly and efficiently explore the state space. However, they suffer sensitivity to the initial solution and slow convergence to the optimal solution, which mean
ieeexplore.ieee.org
0. Abstract
Rapidly random-exploring tree (RRT) is popular path planning algorithm
- However, the quality of the initial path is not guaranteed
- it takes much time to converge to the optimal path.
We propose a novel optimal path planning algorithm based on the convolutional neural network (CNN), namely the neural RRT* (NRRT*).
The NRRT* utilizes a nonuniform sampling distribution generated from a CNN model.
- CNN model can predict the probability distribution of the optimal path on the map, which is used to guide the sampling process.
1. Introduction
Robotic path planning is to plan a collision free path for some specific tasks among a number of static or moving obstacles
The grid-based algorithms including the A* and D* can guarantee finding an optimal path if it exists
- But their time cost and memory usage increase exponentially with the map size and the dimensionality of the state space.
The sampling-based algorithms, such as rapidly random-exploring tree (RRT) have become very popular for efficiently solving high-dimensional and multiconstrained path planning problems.
- An essential factor in determining the performance of the sampling-based planner is the sampling distribution
- usually draw random state samples uniform distribution
A*-RRT* algorithm, where an initial path generated from the A* algorithm is used to guide the sampling process of the RRT* planner
- A* algorithm consumes much more time and memory to find the optimal path
In order to overcome the aforementioned limitations and further take advantage of the A* and the RRT* algorithms
Train a convolutional neural network (CNN) model by learning a large number of optimal paths generated from the A* algorithm.
Trained model can rapidly provide a predicted probability distribution of the optimal path, which is used to guide the sampling process of the RRT* planner.
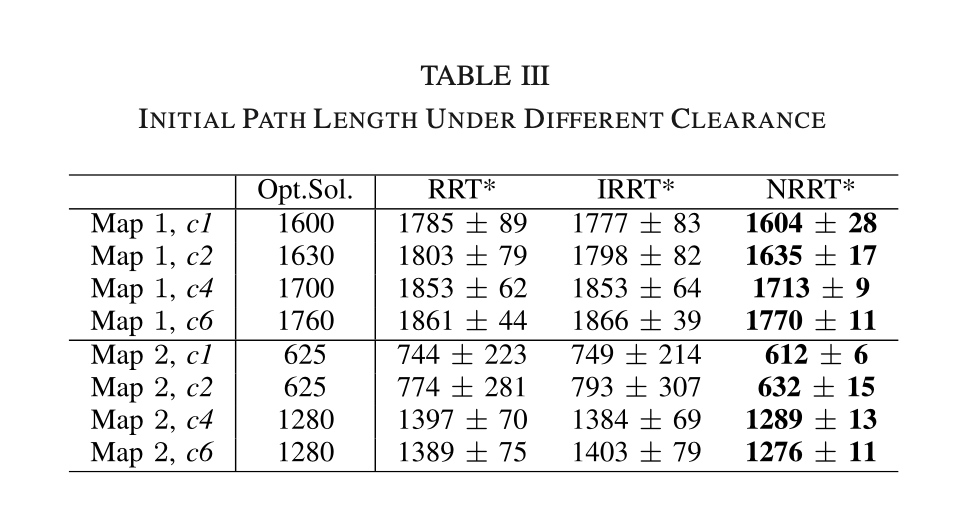
we take into account different clearance and step size in the training process and our CNN model captures the differences so that it can output different probability distributions of the optimal path for the same environment with different parameter settings
2. Prelimiaries
자율주행 논문 리뷰: Neural RRT*: Learning-Based Optimal Path Planning
Author: Joonhee Lim Date: 2022/07/25 논문 원문: https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=9037111 Neural RRT*: Learning-Based Optimal Path Planning Rapidly random-exploring tree (RRT) and its variants are very popular due to their ability to
jhrobotics.tistory.com

draw samples x_rand from the state space using a uniform sampling distribution to construct the feasible path σ∗ in terms of a cost function c(σ).
3. NRRT* Algorithm

Map images which have marked start and goal positions and clearance and step size are given as inputs
Adopt ResNet50 as the backbone of our network encoder
A fully convolutional network can handle input with different resolutions

The model outputs a pretty sharp probability distribution of the optimal path for the current map.
- If we directly use this probability distribution, the probability of completeness of the algorithm is hardly guaranteed.
In order to maintain the ability of the NRRT* to represent the environment with arbitrarily high fidelity,and thus maintain the theoretical completeness guarantee, we also sample from a uniform sampler.
So there are two samplers in the NRRT*, a nonuniform sampler from the neural network model and a uniform sampler.
- set α = 0 (i.e., all samples from the nonuniform sampler)
- the path planner will never find a solution.
- set α = 1 (i.e., all samples from the uniform sampler)
- the performance of the algorithm is the same as the conventional path planner.
- set α = 0.5
- Through a number of simulations, we find that α = 0.5 offers the best balance between ensuring full coverage of the environment and leveraging the learned sample regions.
Generally, the nonuniform sampler can quickly find a feasible path with a few samples.
However, if the nonuniform sampler does not completely identify the solution region, the uniform sampler needs to effectively fill in the gaps.
4. Simulation Results
neural network only takes 50 ms to output a predicted probability distribution of the optimal path whatever the map size, the clearance or the step size. It saves a lot of time cost compared with those which use the A* algorithm to find a prior heuristic path

This shows the illustrations of the predicted sampling distribution for two different maps.
It can be seen that the optimal path lies in the predicted probability distribution. Therefore, using the prediction from the neural network as a nonuniform sampler, the NRRT* can quickly find an initial solution and converge to the optimal solution.
However, it is noted that some prediction results are not perfect.
- in Fig. 4(b) and (f), some regions where the optimal solution cannot lie in are considered as part of the prediction result.
- In Fig. 4(c), (f), and (g), the predicted sampling regions are not continuous.
=> RRTs algorithms have the ability to explore the whole state space and with using two sampling methods, these imperfect predictions have little effect on the performance.
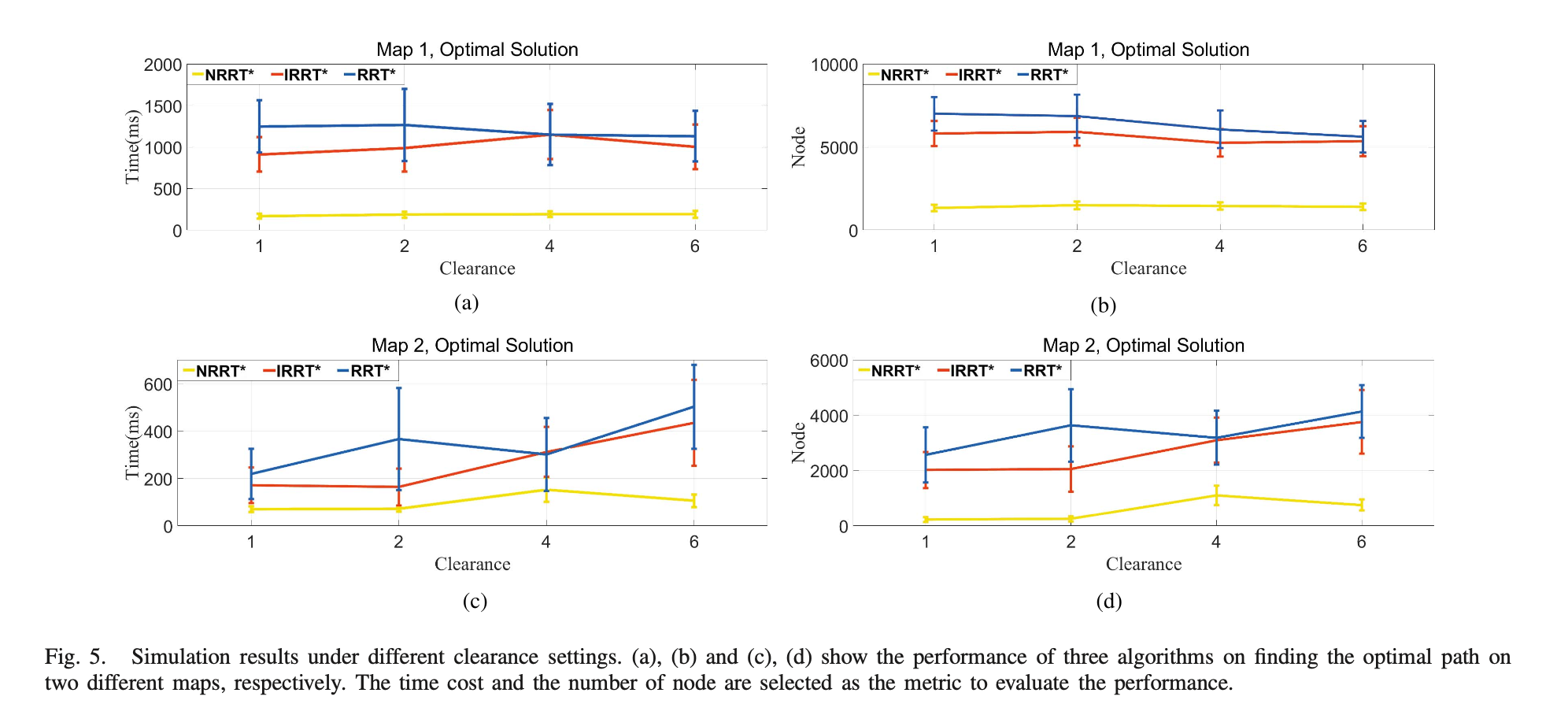
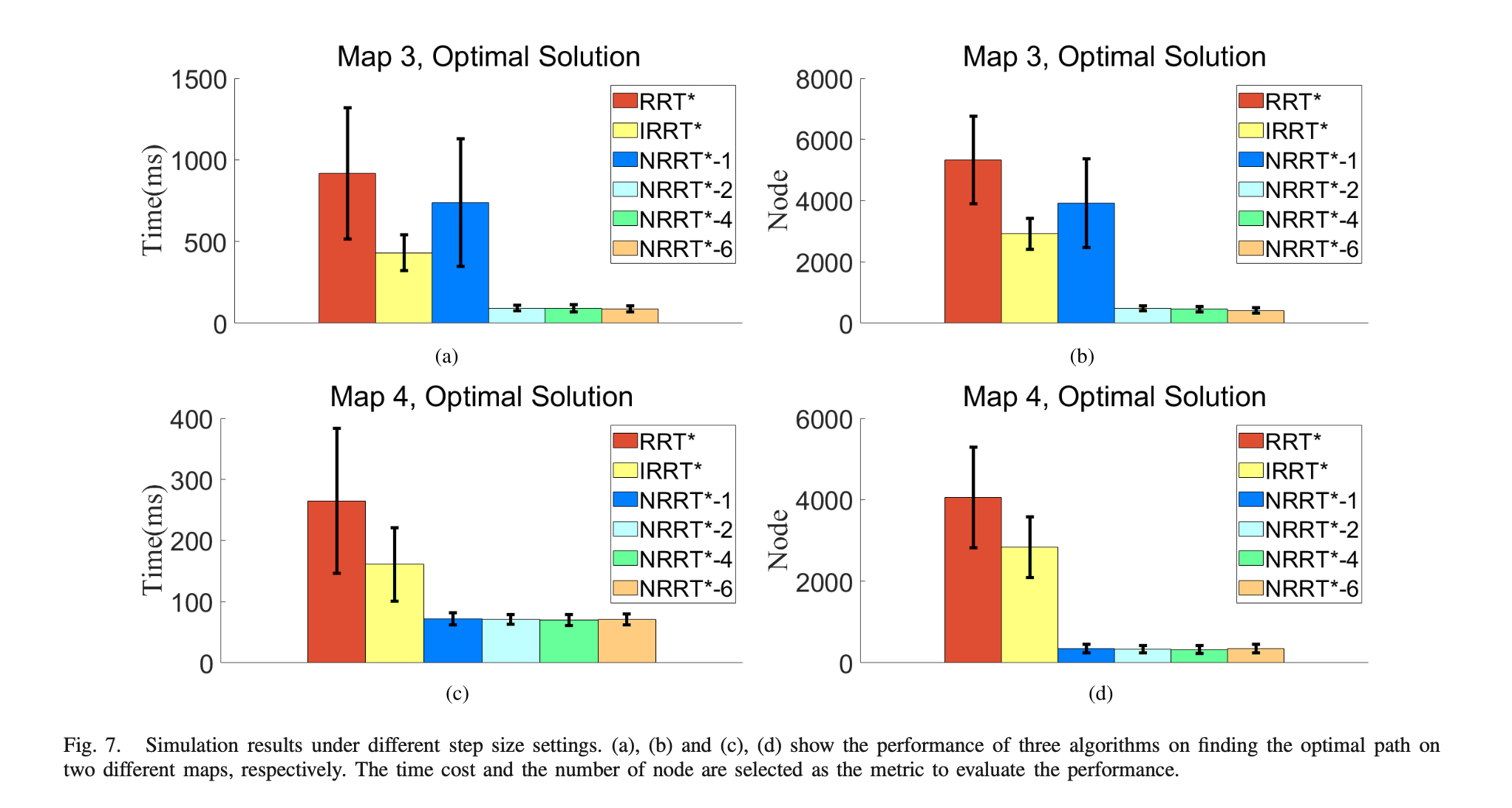
In short, the NRRT* achieves better performance compared with the RRT* and the IRRT*. The reason is that the NRRT* uses a nonuniform sampler to bias samples to the predicted sampling region. This region generated from the neural network contains the optimal path with a large probability, so such a biased sampling process naturally achieves better results.
5. Conclusion and Future Work
Based on the CNN model and the RRT* algorithm, we propose the NRRT* to achieve nonuniform sampling in the path planning process by learning quantities of successful planning cases from the A* algorithm.
the clearance and step size are both considered in the designed CNN model



