1. 모수의 추정, parameter estimation
- 어떤 확률변수 X의 확률 분포를 추정하는 것이 통계적 모델링의 목표이다.
- parametric(모수적) 방법론 : 먼저 x가 어떤 확률 분포를 따른다고 가정한 후, 그 분포를 결정하는 모수를 추정
- nonparametric(비모수적) 방법론 : 특정 확률 분포를 가정하지 않고 데이터에 따라 모델의 구조, 모수의 수가 바뀜
- 어떤 확률변수x가 N(μ, σ2)인 정규분포를 따른다고 가정했을 때, 모수의 평균과 분산은 다음과 같이 inference할 수 있다.
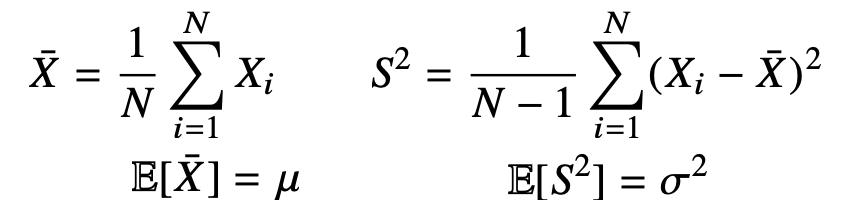
- 표본 평균의 평균 => 모수의 평균, 표본 분산의 평균 => 모수의 분산

- 모집단에서 크기가 n인 표본을 200개 추출했다. 그럼 200개의 표본에 대해서 평균 200개가 나온다. 이 통계량(평균값 혹은 분산값)의 분포를 sampling distribution이라고 하며. 표본 평균의 sampling distribution은 n이 충분히 크다면 정규분포를 따른다 N(모집단의 평균, 모집단의 표준편차^2 / N)
- 이를 central limit theorem이라고 한다. (sampling distribution은 N이 커질 수록 정규분포를 따른다.)
2. 최대 가능도 추정(최대 우도법)
- 가능성이 가장 높은 모수를 찾는 방법
- 확률 변수 X일 때 densitiy, mass function은 f(x;θ) , p(x;θ) 이다. θ(모수)를 이미 알고 있는 상황에서 X=x일 확률을 말한다.
- 하지만 모수 추정에서는 이미 데이터는 알고 있으니 x를 상수벡터로 놓고 θ를 변수로 둔다.
- f(x;θ) == p(x;θ) == L(θ|x)

- x가 꼭 스칼라일 필요는 없다. 벡터일수도 있다 X = [x1, x2, ...]일때는 P(X|θ)가 곱으로 구해진다.
- 모수가 어떤 분포를 따를 것이라고 가정하면 p(x|θ)를 구할 수 있다.
-이렇게 가정한 분포에 X=xi일때의 확률을 likelihood라고 한다.
- 모든 관측값들의 likelihood 곱의 최대를 구한다는 즉, 표본 X를 뽑을 확률이 가장 높은 θ를 구한다는 말이다.
- 보통은 log를 씌워서 log-likelihood로 대신 구한다. 덧셈으로 계산할 수 있게 된다.
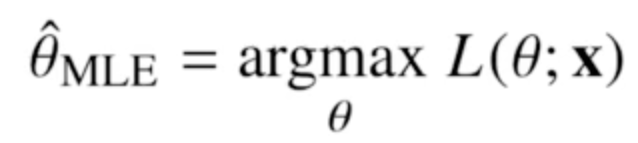
- 표본 X가 뽑힐 확률이 가장 높은 θ를 찾는다 == likelihood 값의 최대를 찾는다.


- 로그 가능도 추정을 활용하면 deep learning 모델을 학습시킬 수 있다. (일반적인 gradient descent말고)

- 모델이 학습하는 확률 분포 vs 데이터에서 관찰되는 확률분포
- 두 분포의 거리를 최소화 하도록 학습이 되어야 좋을 것이다.
- 손실 함수를 무엇으로 사용하냐에 따라서 두 분포의 거리를 최소화 하는 방향이 달라진다.
- 예를 들면 y_prediction - y_label의 분산을 최소화 하는 방향으로 학습이 되길 원할 수도 있고 y_prediction의 불확실성을 최소화 하는 방향으로 학습이 되길 원할 수도 있다.
- 즉 우리가 어떤 Loss function을 정의하냐에 따라 확률론에 기반해서 모델이 학습하는 방향이 결정된다.
- 하나의 데이터 공간에 확률 분포 P(x) 와 Q(x)가 있을 때, 두 확률 분포의 distance를 구하는 방법으로 쿨백-라이블러 발산 (Kullback-Leibler Divergence, KL)이 있다.

- 정답 레이블을 P, 모델 예측을 Q라고 했을 때, maximum likelihood estimation은 결국 이 쿨백-라이블러 발산(거리)를 최소화 하는 것과 같다.
'boostcamp AI tech > boostcamp AI' 카테고리의 다른 글
| PyTorch Project (0) | 2023.11.13 |
|---|---|
| PyTorch Basics (0) | 2023.11.13 |
| Bayes Theorem (0) | 2023.11.10 |
| BPTT for RNN (0) | 2023.08.26 |
| Recurrent Neural Networks (0) | 2023.08.23 |



