- 이미지의 한 픽셀이 (r,g,b)를 갖는다고 하면 한 픽셀이 가질 수 있는 값의 경우의 수는 256*256*256이다.
- 이 경우의 확률 분포로 표현하기 위한 파라미터 수는 256*256*256-1개이다. 너무 많다.
- 10 by 10 이미지라면 (256*256*256-1)^100 -1 개의 파라미터가 필요하다.

- 그럼 채널 수를 줄인 흑백 (28,28) 이미지라고 했을 때 이미지가 가질 수 있는 경우의 수는 2^784 가지나 된다. 이 모든 경우의 수를 판단하기 위해서는 파라미터 수가 2^784-1개 필요하다. 역시 너무 많다.
- 이런 간단한 이미지에 대해서도 이미지가 가질 수 있는 전체 경우의 수를 고려한 확률분포를 모델이 학습하는 것은 거의 불가능 하다.
- 만약에 픽셀끼리의 값이 independent하다면 어떨까? 한 픽셀의 값와 그 주변, 다른 픽셀의 값은 아무 관계가 없다고 보는 것이다.
- P(x1, x2, ..., xn) = p(x1) p(x2) p(x3), ..., p(xn)
- 여전히 이미지가 가지는 경우의 수는 2^784이지만 이를 포현하기 위한 파라미터 수는 784개로 확 줄어들어버린다.
- 이렇게 Independent assumption 가지고서는 분포를 모델이 학습했다고 하더라도 의미있는 결과를 만들어낸다고 볼 수 없다. 각 픽셀간의 관계가 다 사라져 버렸기 때문이다.
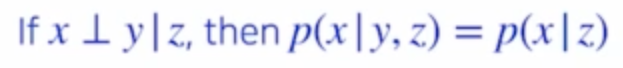
- 그래서 중간은 찾은 것이 conditional independence이다.
- x ㅗ y | z : z라는 random variable이 주어졌을 때, x와 y가 independent하다는 뜻이다.
- 따라서 y, z가 함께 주어지면 x를 y로 부터 떼어낼 수 있게 된다. 이를 아래 조건부 확률 계산에 활용할 수 있다.
- p(x_1, ..., x_n) = p(x_1) p(x_2 | x_1) p(x_3 | x_1, x_2), ..., p(x_n | x_1, ..., x_n-1)
- 즉 independent assumption으로 파라미터를 줄이면서 jointly distributed된 분포를 사용하게 되었다.

- 0,1 이미지일 경우, Joint distribution에서 필요한 파라미터 수는 다음과 같다.
- P(X1) : parameter 1개
- P(X2 | X1) : parameter 2개
- P(X3 | X1, X2) : parameter 4개
- total needed parameters : 2^n -1 개

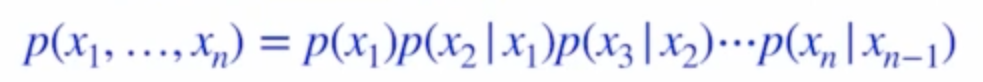
- 여기에 위와 같은 Markov assumption을 적용하면 chain rule에 대한 식이 위 처럼 변한다.
- 그럼 total parameter수는 2n-1개가 된다.
- 완전히 independent하다고 가정했을 때와 전부 independent하지 않다고 가정했을 때의 중간 지점을 찾았다.
1. Autoregressive Models
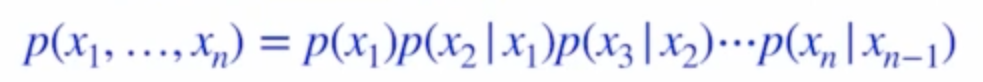
- p(x1) 구하고, x1에 의존하는 x2의 확률 p(x2 | x1)을 구하고 이어서 p(x3 | x2)를 구하고..
- 이렇게 순차적으로 한 픽셀씩 완성해가는, 순차적으로 정의되는 모델을 autoregressive model이라고 한다. 즉 과거 값들을 바탕으로 현재 값의 조건부 확률을 계산한다.
2. NADE : Neural Autoregressive Density Estimator
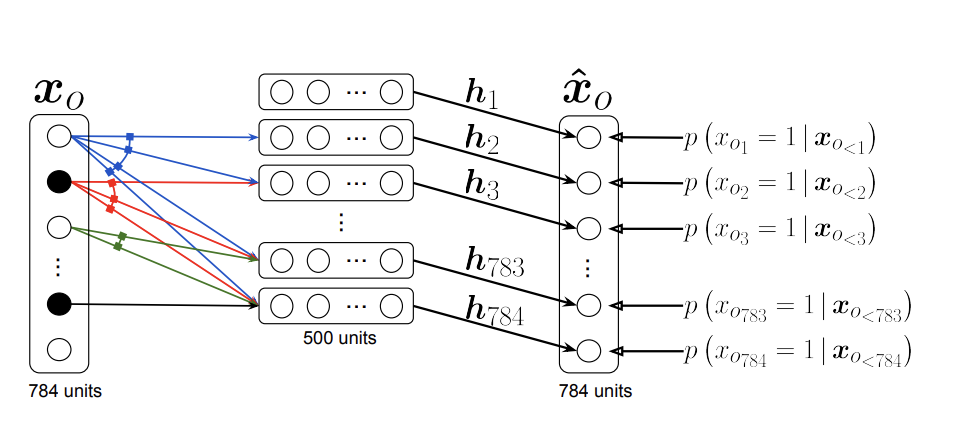

- 입력으로 이미지를 받았을 때 해당 이미지의 probability densitiy, Joint distribution을 구하도록 neural network를 학습 시켰다. 즉 이미지의 픽셀간의 joint distribution을 학습한다. 이런걸 explicit model이라고 한다.
- 예를 들어 GAN처럼 이미지를 생성은 하는데 probability densitiy를 모르는 경우를 Implicit model이라고 한다.
- 서로 다른 evaluation metric이 등장할때마다 새로운 model들이 등장했다.
3. Maximum Likelihood Learning
- 모델이 학습한(데이터를 생성해내는) 분포와 데이터에 존재하는 분포와의 차이를 최소화 하는 개념이다. (best-approximating density)
- 두 분포의 거리를 정의하는 대표적인 예로 KL divergence가 있다.


- 결국은 뒤에 항을 최대화 하는 방향으로 parameter를 구하도록 한다.

- 그런데 원래는 모든 가능한 데이터 x에 대해서 P(x)를 구해야 하는데 그건 불가능하니까 training dataset D만 보고 추정을 한다.
- 이를 empirical log-likelihood라고 하고 이걸 가지고 추정한다. (ERM, Empirical Risk Minimization)
- 하지만 우리가 추정하려는 확률분포로 선택할 수 있는게 몇 개 없다. 가우시안 분포를 제일 만만하게 사용했으나 역시 표현력이 높지 않은 분포들만 사용했기 때문에 성능이 별로 좋지 않다.
4. Variational Inference and Variational Autoencoder

- 어떤 분포를 찾고 싶은데 너무 복잡해서 내가 모델링 하기가 어렵다.(posterior distribution) 그러니 (variational distribution)로 근사해서 모델링한다.
- p_θ(z|x), posterior distribution 대신 encoder가 q_φ(z|x), variational distribution을 학습하도록 한다.
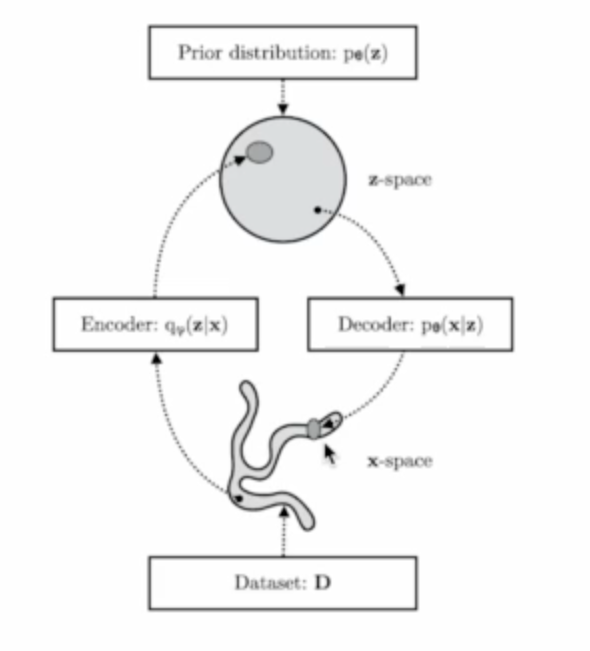
- 그럼 그 p_e(z), Latent 공간에서의 샘플을 가지고 decoder가 결과를 만들었을 때 posterior distribution와 비슷하도록 한다.

- 어쨌든 입력으로 들어온 데이터들이 나올 확률을 최대로 하도록 하는게 목표다.
- variational gap은 수식으로 풀기조차 어려워서 계산이 어렵다.
- 그러니 상대적으로 계산할 수 있는 ELBO 부분을 최대로 해서 variation gap을 줄이도록 한다.

- q_φ(z|x) :x가 입력으로 주어졌을 때, 인코더를 통과해서 만들어진 latent vector z
- p_θ(x|z) : latent vector z가 들어갔을때, 나온 x
- 위 두 부분이 인코더-디코더를 거친 결과로 볼 수 있기 때문에 reconstruction term이라고 한다. 이걸 늘린다.
- latent distribution과 사전에 정해둔 prior distribution을 비슷하게 함으로써 prior fitting term을 줄인다. 많은 경우 prior distribution은 가우시안을 활용한다.
5. Generative Adversarial Network

- z를 가지고 generator가 만든 결과 G(z)를 D가 보고 1이라고 하면 속이기 성공이다 그럼 V값은 음의 무한대가 되므로 V를 최소화하는 G를 찾으면 되고
- 반대로 D가 G(z)를 보고 0, 가짜라고 잘 분별하면 V는 0, 최대값을 갖는다. 따라서 V를 최대로하는 D를 찾는다.

- 두 변수에 대해서 최소 최대를 구하기 어려우니까 일단 G가 고정이라고 생각하고 D를 Optimize해보자.


- G를 고정이라고 생각하고 위 식을 최대로 하는 D를 찾아보자. 미분해서 0되는 점을 찾으면된다. 그 지점에서의 가장 Optimal한 Discriminator는 위 처럼 생겼다.
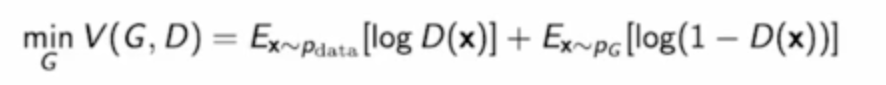
- 그럼 최적의 D를 가지고 이번에는 Generator의 목적함수에 넣어보자.

- 알 수 없지만 존재한다고 가정하고 있는 데이터의 distribution과 최적화하려는 Generator의 distribution의 JSD가 나온다.
- 즉 이 Jenson-Shannon divergence를 최소화 하는 방향으로 모델이 학습하면 된다.
- 이렇게 괴롭게 수식을 살펴보고 있는 이유는 딱 하나다. 생성모델이 학습하는 함수가 결국엔 분포로 해석될 수 있다는 것이다.
6. Diffusion Models

- forward : 이미지에 noise를 점점 추가하면서 noise화 시킨다.
- forward과정은 이미 정해져있는 과정이다. 모델이 학습하는건 Reverse 과정이다. 즉 복원하는 과정을 학습한다.
- 한번에 이게 이루어지는 것은 아니다. 예를들어 1000번의 step동안 조금씩 노이즈를 넣고. 다시 1000번에 걸처서 노이즈에서 이미지로 바꾸는 과정을 거친다.
'boostcamp AI tech > boostcamp AI' 카테고리의 다른 글
| Word Embedding - Word2Vec, GloVe (1) | 2023.11.27 |
|---|---|
| Naive-Bayse Classifier (1) | 2023.11.27 |
| Transformer (2) | 2023.11.23 |
| Short History of Sequential Model (1) | 2023.11.23 |
| Short History of Detection Model (0) | 2023.11.22 |


