1. Cost functions
- The Loss function computes the errors of a single training example.
- The Cost Function computes the average of the loss functions for all the examples.
2. Gradient descent
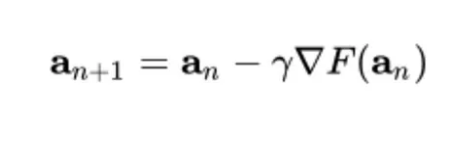
- ∇F(a n) = the gradient term indicates the direction of the steepest descent, The direction for the next position
- Mini-batch gradient descent: It combines concepts from the first two. It divides the dataset with the training examples into sample batch sizes. It then performs updates on each of those batches.
- 두 벡터 사이의 거리를 정의 하는 방법은 여러가지가 있다. 정의에 따라서 벡터를 바라보는 관점이나, 성질이 달라진다.
- L1-norm(sum of the magnitude of vectors), L2-norm(Eucldian distance)
- 행렬의 각 row를 d차원 공간의 점으로 해석하면 행렬은 d차원 위에 있는 여러 점들로 해석할 수 있다. 그럼 행렬의 곱을 transformation으로 해석할 수도 있다. A * T = A'
- np.inner() : 원래 행렬곱은 행, 열 간의 내적이다. 하지만 inner()함수는 두 행렬의 행간 내적으로 계산한다.
- matrix의 determinent가 0이 아닌 경우, nxn의 모양일 때, inverse matrix를 구해서 방정식을 풀 수 있다. Ax = b
- 그렇지 않은 경우에는 Moore-penrose, pseudo-inverse matrix를 구해서 방정식의 해를 구할 수 있다. 만약 변수의 개수보다 방정식의 개수가 많은 경우는 근사값을 구하게 된다.
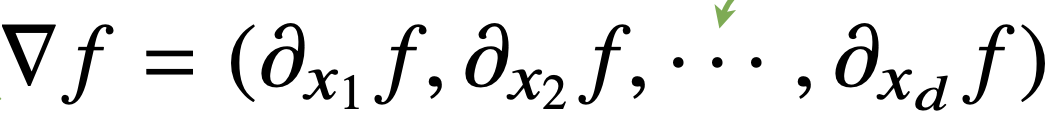
- gradient vector equation
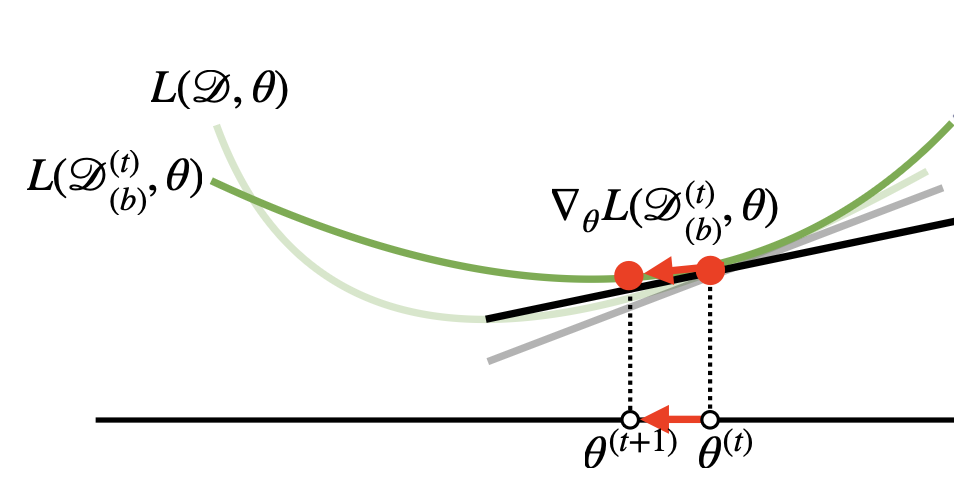
- batch gradient descent : 모든 데이터에 대한 Loss를 weight에 대해 미분하여 gradient를 구한다. epoch마다 Loss 함수가 변하지 않는다. 따라서 잘못된 convex에 갇힐 수 있다.
- 반면 minibatch stochastic gradient descent의 경우 minibatch마다(iteration마다) Loss 함수가 바뀐다. 따라서 local minima를 피해갈 수 있다. (새로운 일부 데이터 D(b)에 대한 Loss 함수에서는 convex의 위치가 달라지니까)
- 가장 간단한 loss를 예로 생각해보자. L(y - Xβ) 에서 전체 데이터 X를 쓰는 경우에는 학습이 반복돼도 Loss가 달라지지 않는다. 하지만 minibatch학습시 iteration마다 X(b)로 달라지면 Loss는 L(y-X(b)β)로 바뀌고 β에 대해 미분했을 때 gradient도 달라진다.
- gradient descent로 regression을 구현하는데 있어서 loss를 L2-norm으로 가정하고 단계를 생각해보자.
- n개의 데이터에 대해 forward propagation
- n개의 데이터에 대한 loss n개
- n개의 데이터에 대한 gradient n개
- n개의 gradient의 평균으로 w 업데이트
- loss값의 평균을 기록
'boostcamp AI tech > boostcamp AI' 카테고리의 다른 글
| BPTT for RNN (0) | 2023.08.26 |
|---|---|
| Recurrent Neural Networks (0) | 2023.08.23 |
| Convolutional Neural Network (0) | 2023.08.23 |
| Autoencoder (0) | 2023.08.17 |
| Why do we need activation function? (0) | 2023.08.16 |



