
In this section, we will implement the linear regression model which we've implemented before by using high-level APIs of deep learning frameworks.
- Generating Dataset
- Reading the dataset (minibatches)
- Defining the Model
- Initializing Model Parameters
- Defining the Loss Function
- Defining the Optimization algorithm
- Training
1. Generating Dataset
Generate the same dataset we've made before.


2. Reading the dataset (minibatches)

3. Defining the Model
We can use a frameworkʼs predefined layers

Though we only have one layer using sequential we can define a container for serveral layers which will be chained Given input data, a Sequential instance passes it through the first layer, in turn passing the output as the second layerʼs input and so forth.
In PyTorch, the fully-connected layer is defined in the Linear class.
two ar- guments into nn.Linear : The first one specifies the input feature dimension, which is 2, and the second one is the output feature dimension, which is a single scalar and therefore 1.
4. Initializing Model parameters
Here we specify that each weight parameter should be randomly sampled from a normal distribution with mean 0 and standard deviation 0.01

5. Defining the loss function
By default it returns the average loss over examples.

6. Defining the optimization algorithm

7. Training
• Generate predictions by calling net(X) and calculate the loss l (the forward propagation).
• Calculate gradients by running the backpropagation.
• Update the model parameters by invoking our optimizer.

To access parameters, we first access the layer that we need from net and then access that layerʼs weights and bias.
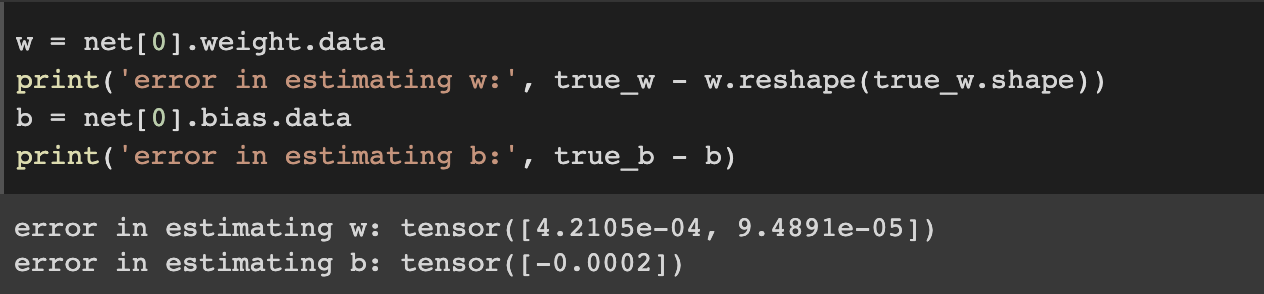
you can access the gradient of net[0].weight like "net[0].weight.grad"
'ComputerScience > Machine Learning' 카테고리의 다른 글
| Deep Learning - 2.5 The Image Classification Dataset (0) | 2022.08.19 |
|---|---|
| Deep Learning - 2.4 Softmax Regression (0) | 2022.08.18 |
| Deep Learning - 2.2 Linear Regression Implementation from Scratch (0) | 2022.08.13 |
| Deep Learning - 2.1 Linear Regression (0) | 2022.08.11 |
| Deep Learning - 1.6 Probability (0) | 2022.08.09 |



