1. Game Tree
- 지난시간에 배웠던 탐색 알고리즘을 응용하여 실제 게임에 접목해보자.

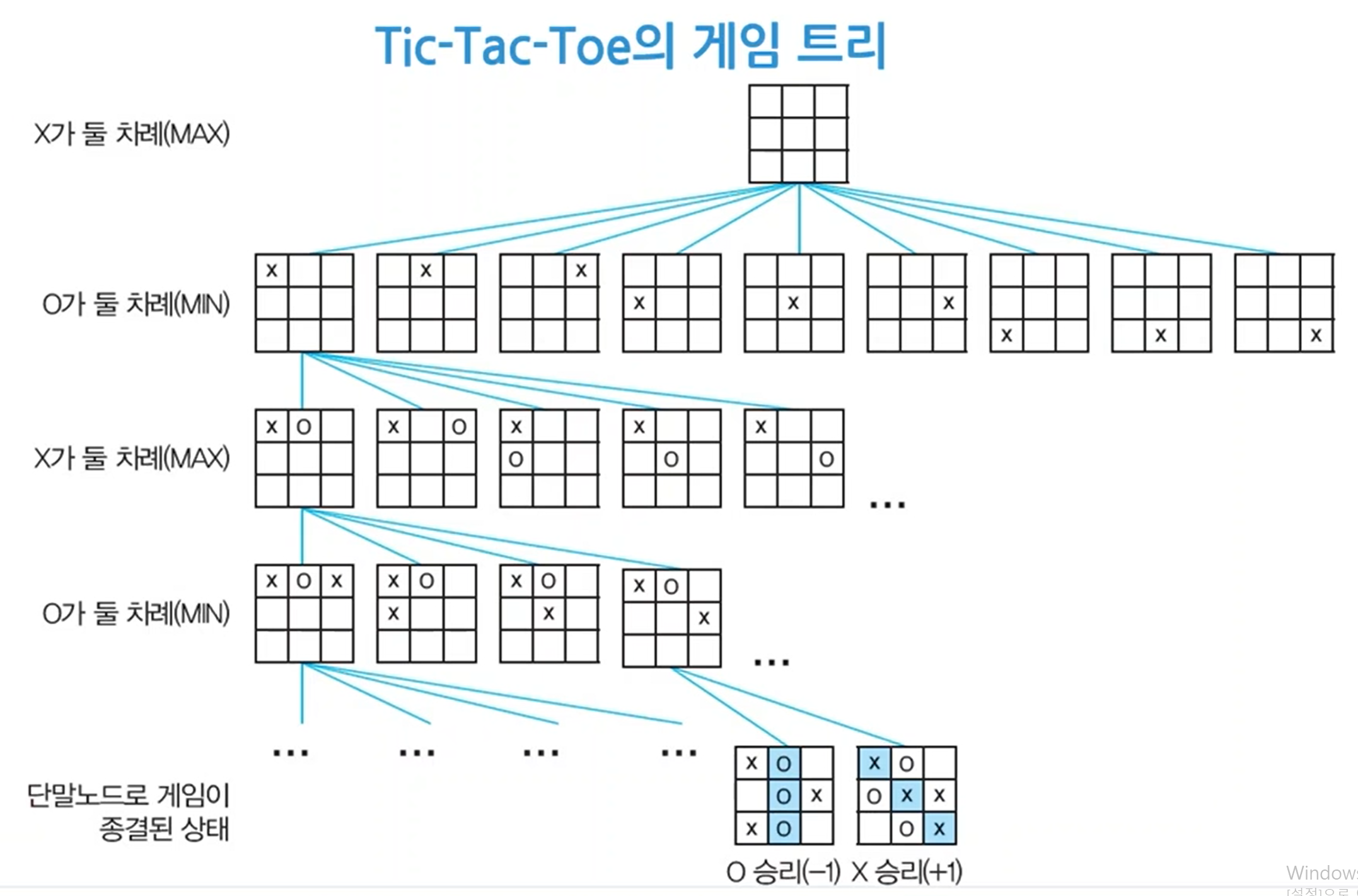
- tic tac toe 게임에서 가능한 모든 경우들을 tree로 나타내면 위와 같다.
2. MiniMax 알고리즘
- 만약 tic-tac-toe 게임상황에서 이기는 전략을 짜고 싶다면 어떻게 해야할까?
- MiniMax알고리즘은 상대 플레이어가 항상 최선의 수를 둔다는 가정하에 이기는 전략을 찾는 알고리즘이다.
- 먼저 다른 예시를 통해 MiniMax알고리즘의 동작을 살펴보자.
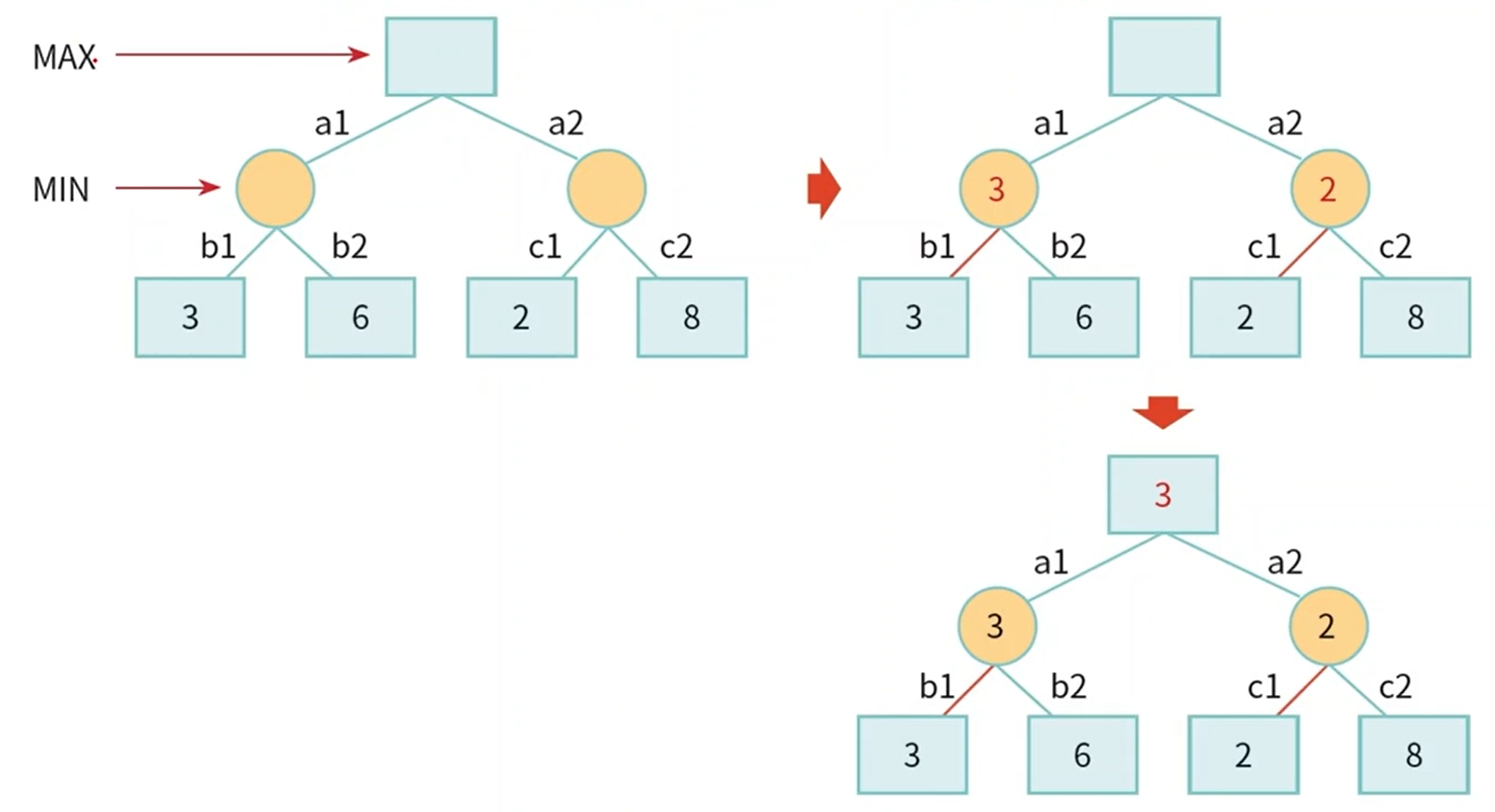
- 맨 밑의 leaf node에서 상위 노드로 값을 전달하는데 Min노드 이면 작은 값을 Max노드이면 큰값을 받는다.
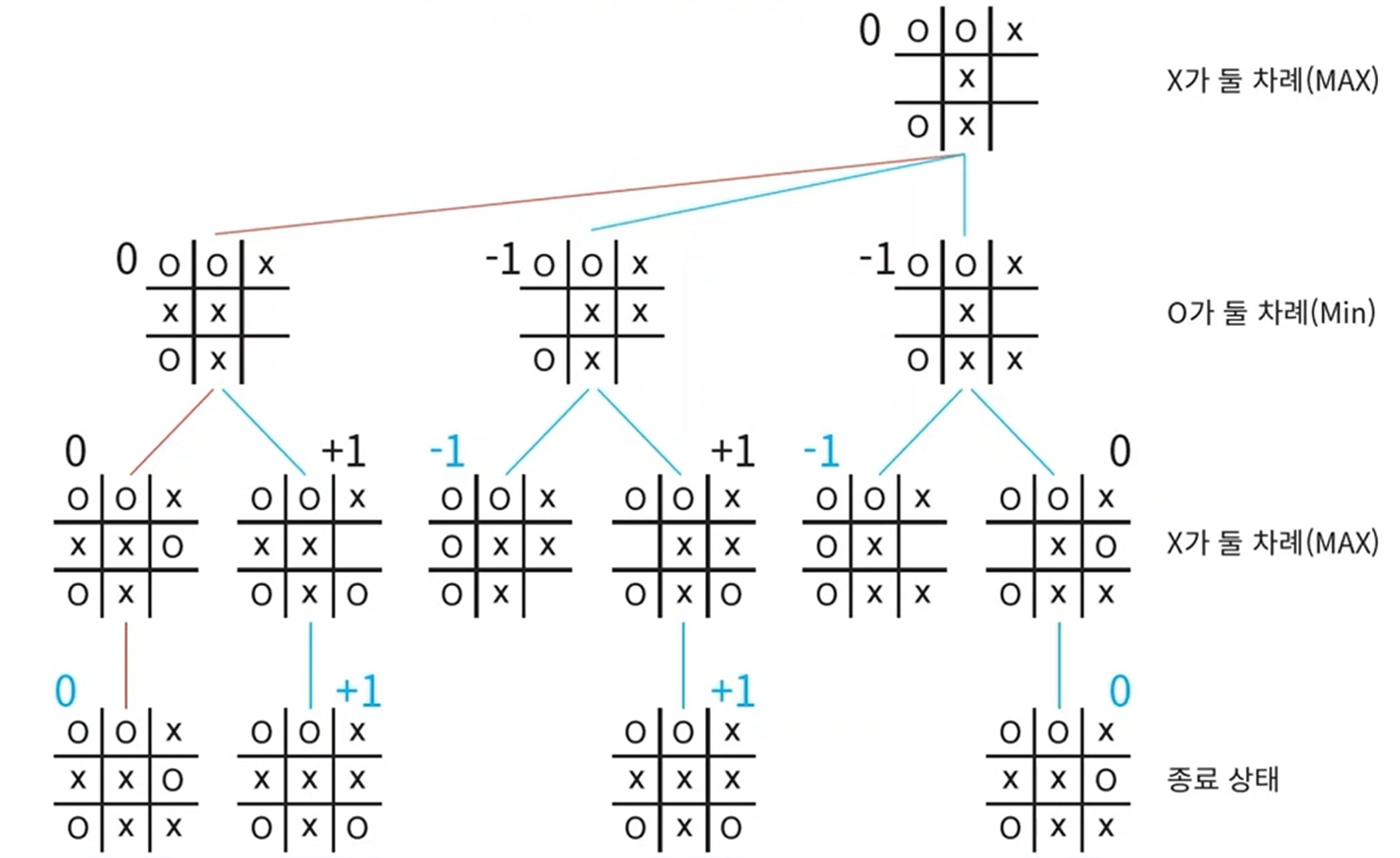
- MiniMax알고리즘에 따라 각 노드의 state를 0, -1, 1로 표시한다고 하면 다음과 같다.
- 이제 게임을 할 때 Max가 이기고자 한다면 이동가능한 노드중에서 항상 최선의 선택(+1)을 찾아서 나아가면 된다.
- 반대로 Min이 이기고자 한다면 이동 가능한 노드 중에서 항상 최선의 선택으로 -1을 찾아가면 된다.

- 하지만 이 알고리즘은 특정 노드에서 최선의 선택을 찾기위해 깊이 우선 탐색을 진행한다. 즉 트리의 길이가 길어지거나 선택 가능한 노드수가 증가하면 복잡도는 O(선택가능 노드수^깊이)이 된다.
3. 알파 베타 - 가지치기
- Minimax의 높은 시간 복잡도를 줄일 수 있는 방법이다.
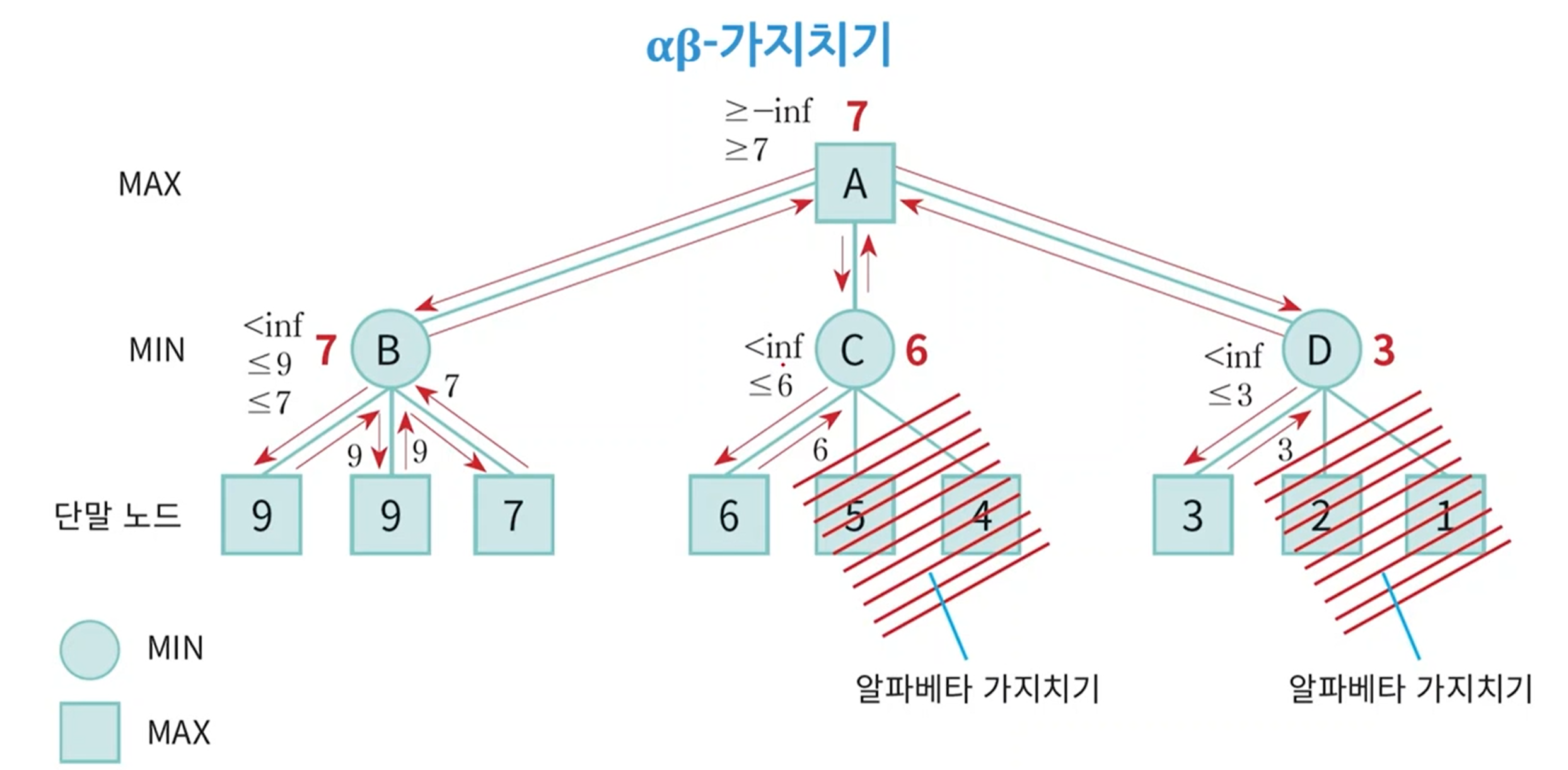
- A는 B, C, D중에서 가장 큰 값을 선택해야 한다.
- 가장먼저 살펴볼 B의 value는 7이다. 세개의 자식들을 탐색해서 나온 결과(9, 9, 7)중 최소값에 해당한다.
- 이제 C를 살펴보자. C의 첫번째 자식이 6이라는 결과를 냈다고 해보자. A입장에서는 B, C, D중에 최대값을 취해야 한다.
- 그런데 C의 첫번째 자식이 6이라는 말은 6보다는 큰 수가 C가 될 수 없으며 A한테 올려보낼 수 있는 수는 아무리 커봐야 6이 된다는 것이다.
- 하지만 B가 7인걸 이미 알기 때문에 C는 더이상 탐색을 진행할 필요가 없게 된다.
- 이렇게 탐색해야하는 경우의 수를 줄여나가는 것을 알파 베타 가지치기라고 한다.

- 이 알고리즘은 알파와 베타값을 재귀 호출시 전달해준다.
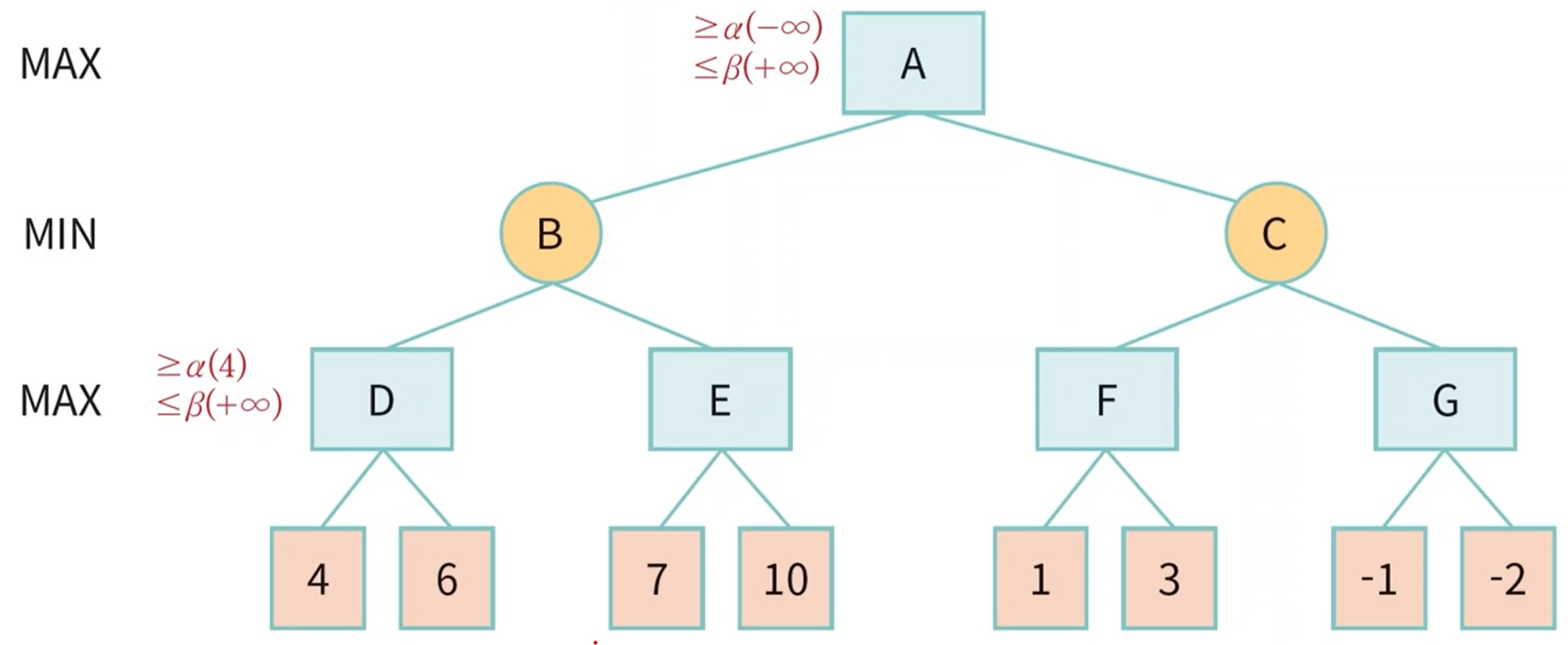
- 초기 알파는 -무한, 베타는 +무한이다.
- 자식 노드로 탐색을 이어갈 때마다 알파 베타를 전달해준다.
- MAX는 알파만 업데이트하고 MIN은 베타만 업데이트 한다.

- E는 7보다 크거나 같다. 그런데 B가 6보다 작거나 같기때문에 E의 자식을 더 이상 탐색할 필요가 없다.

- C는 결국 3보다 작거나 같다. B가 6이기때문에 더 이상 C의 자식을 탐색할 필요가 없다.
4. 불완전한 결정
- Minimax 알고리즘은 탐색 공간 전체를 탐색하는 것이 전제되어 있다.
- 아무리 알파베타 가지치기 처럼 최적화를 하려고 해도 제한된 리소스로 모든 경우를 탐색하는 것은 한계가 있다.
- 그렇다면 주어진 시간안에 가장 매력적으로 보이는 선택지를 고르도록 heuristic하게 선택을 해야 할 것이다.
- 즉 예를 들면 아직 자식 노드를 탐색하지는 않았지만 evaluation function으로 그 자식노드로 나아갔을 때의 가치를 평가하는 것이다.
- 아래 그림을 보면 실제로 자식 노드의 경우들을 다 따져보지는 않았지만 승리 가능성이 더 높아보이는 수를 두도록 한다.
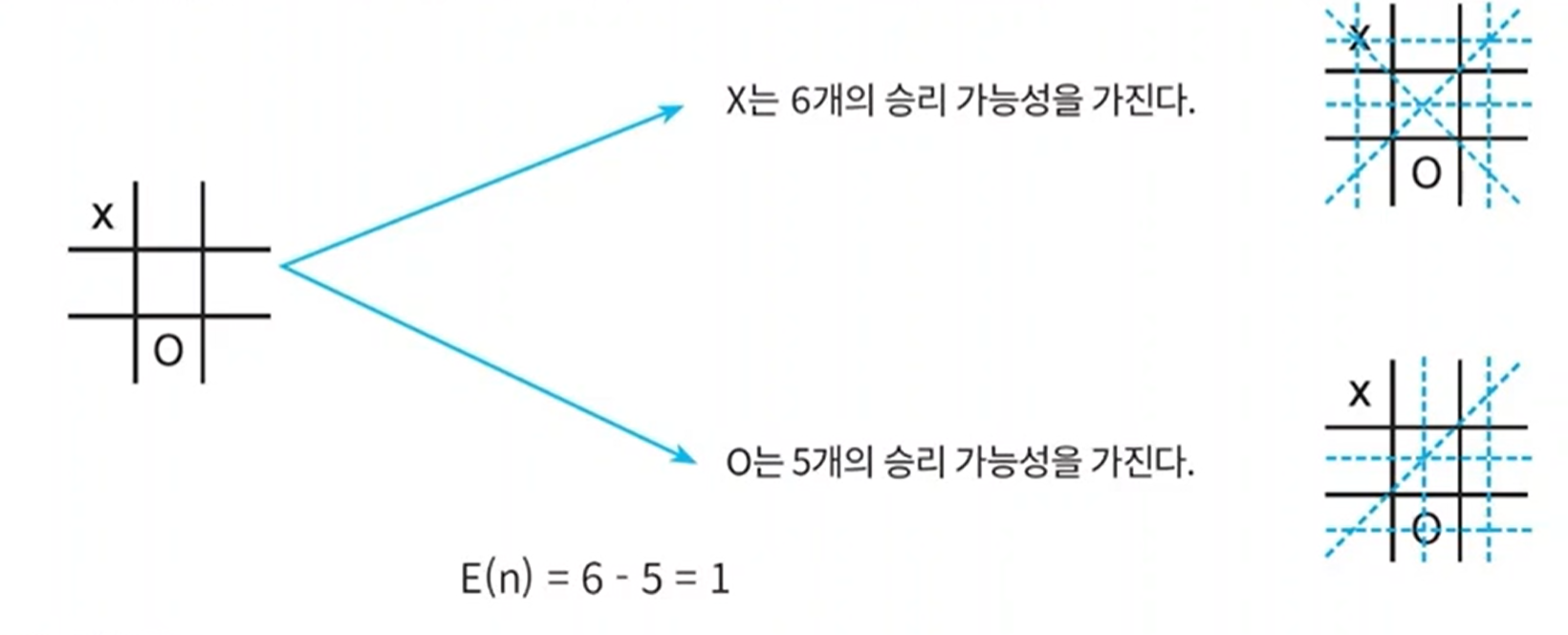
- 이렇게 불완전한 결정으로 다음 수를 놓고자 한다면 치밀한 evaluation function을 설계해야 할 것이다.
'ComputerScience > Machine Learning' 카테고리의 다른 글
| AI - 5. Fuzzy Logic (0) | 2021.10.01 |
|---|---|
| AI - 4. 전문가 시스템 (0) | 2021.09.17 |
| Deep Learning 1-4-2 (0) | 2021.09.14 |
| Deep Learning 1-4-1 (0) | 2021.09.14 |
| Deep Learning 1-3-2 (0) | 2021.09.14 |



