
we will learn how to incorporate nonlinearities to build expressive multilayer neural network architectures.
MLP adds one or multiple fully-connected hidden layers between the output and input layers and transforms the output of the hidden layer via an activation function.
- Hidden Layers
- Activation Functions
1 Hidden Layers
MLPs can capture complex interactions among our inputs via their hidden neurons, which depend on the values of each of the inputs. (which was difficult for linear model)
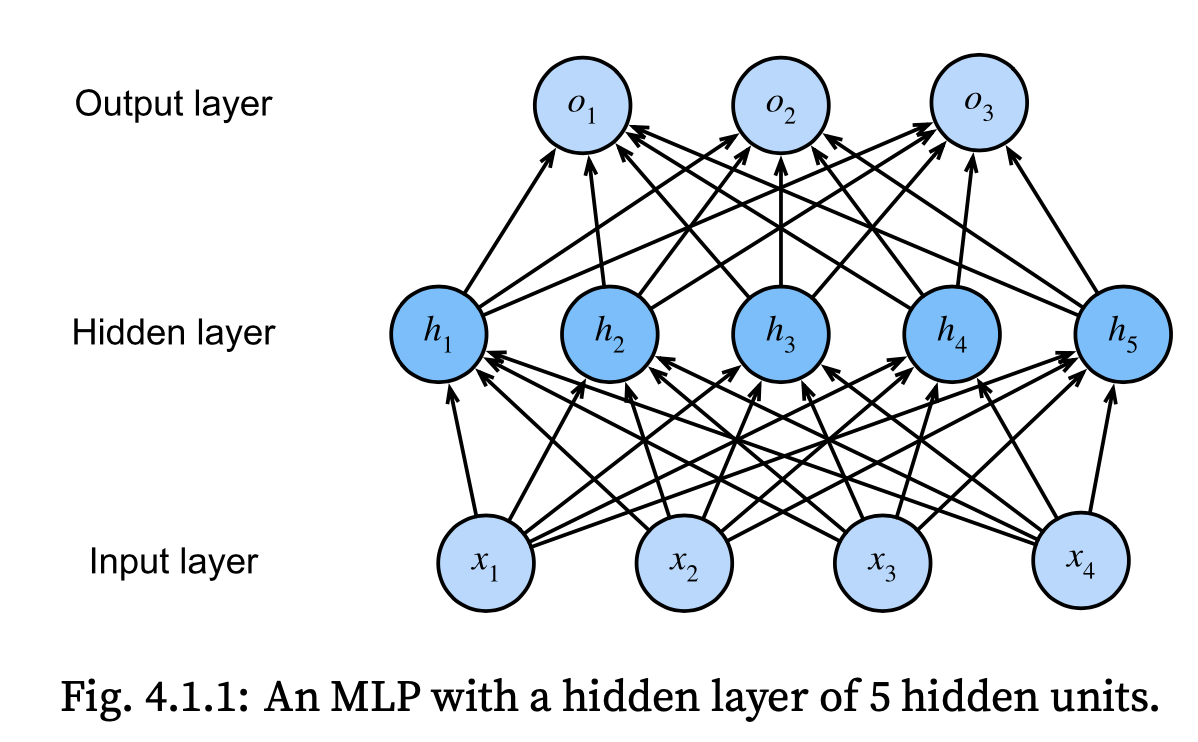
This MLP has 4 inputs, 3 outputs, and its hidden layer contains 5 hidden units. Since the input layer does not involve any calculations, producing outputs with this network requires implementing the computations for both the hidden and output layers; thus, the number of layers in this MLP is 2
X ∈ Rn×d, (minibatch of n examples, each example has d inputs (features).
hidden layer has h hidden units, denote by H ∈ Rn×h (outputs of the hidden layer)
Since the hidden and output layers are both fully connected, we have hidden-layer weights W(1) ∈ Rd×h and biases b(1) ∈ R1×h and output-layer weights W(2) ∈ Rh×q and biases b(2) ∈ R1×q.

An affine function of an affine function is itself an affine function.
So we gained nothing by stacking more hidden layers. Our linear model was already capable of representing any affine function.
In order to realize the potential of multilayer architectures, we need one more key ingredient: a nonlinear activation function σ to be applied to each hidden unit following the affine transformation.
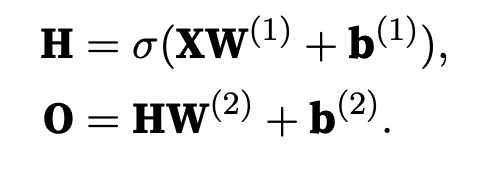
2. Activity Functions
Activation functions decide whether a neuron should be activated or not by calculating the weighted sum and further adding bias with it
They are differetiable and add non-linearity
ReLU Function
Rectified linear unit (ReLU) is defined as the maximum of that element and 0: retains only positive elements and discards all negative elements by setting the corresponding activations to 0
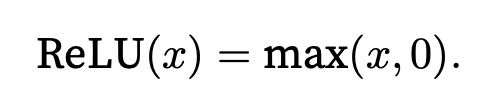

When the input is negative, the derivative of the ReLU function is 0, and when the input is positive, the derivative of the ReLU function is 1.
ReLU function is not differentiable when the input takes value precisely equal to 0. In these cases, we default to the left-hand-side derivative and say that the derivative is 0 when the input is 0.
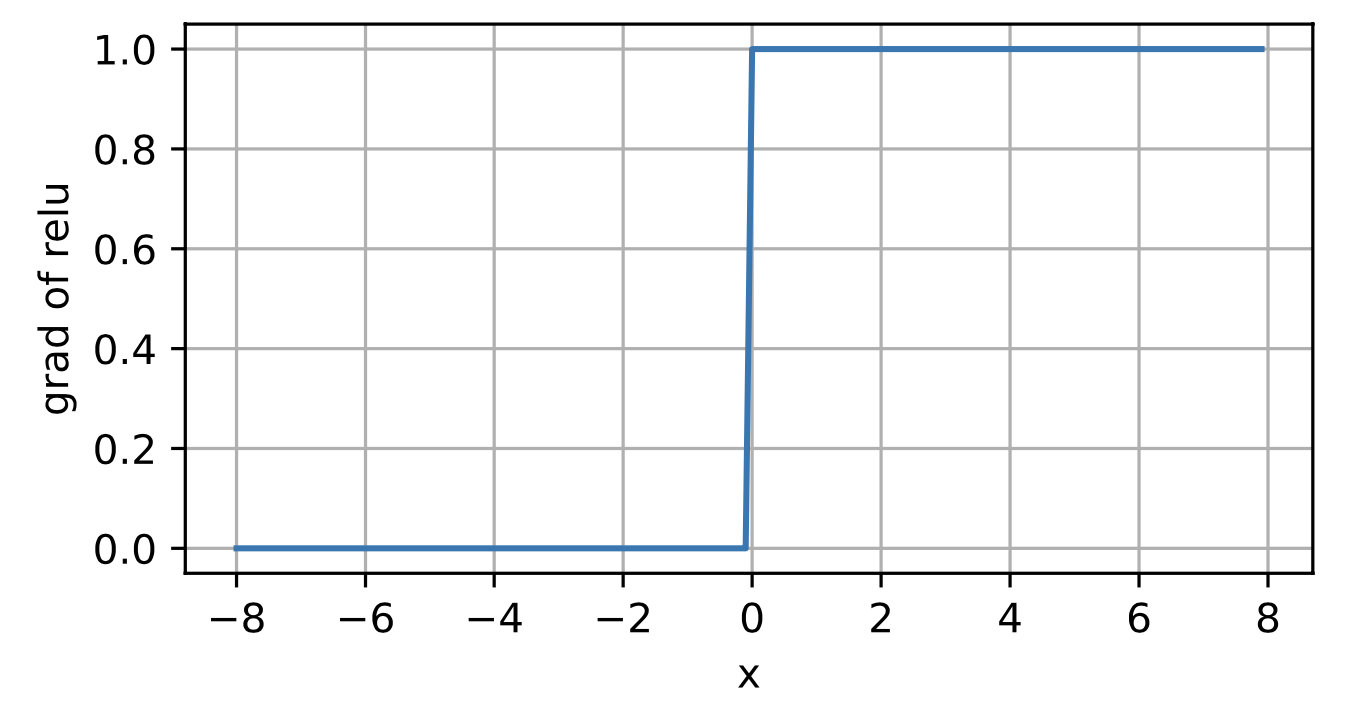
the derivative of the ReLU function
This makes optimization better behaved and it mitigated the well-documented problem of vanishing gradients that plagued previous versions of neural networks (more on this later).
Sigmoid
The sigmoid function transforms its inputs, for which values lie in the domain R, to outputs that lie on the interval (0, 1). For that reason, the sigmoid is often called a squashing function: it squashes any input in the range (-inf, inf) to some value in the range (0, 1):
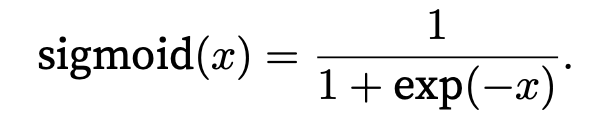
Sigmoids are still widely used as activation functions on the output units, when we want to interpret the outputs as probabilities for binary classification problems (you can think of the sigmoid as a special case of the softmax).
However, the sigmoid has mostly been replaced by the simpler and more easily train- able ReLU for most use in hidden layers.


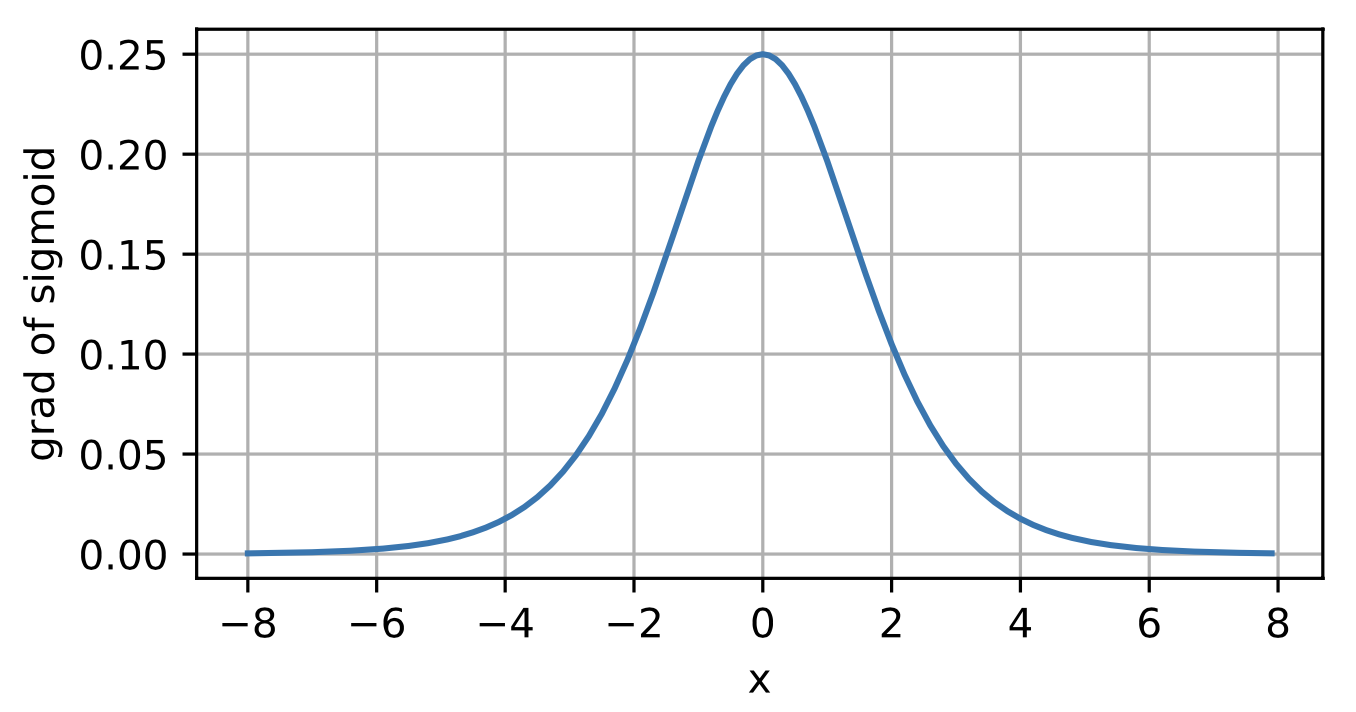
Note that when the input is 0, the deriva- tive of the sigmoid function reaches a maximum of 0.25.
Tanh
tanh (hyperbolic tangent) function squashes its inputs, transforming them into elements on the interval between -1 and 1


'ComputerScience > Machine Learning' 카테고리의 다른 글
| Deep Learning - 3.4 Model Selection, Underfitting, Overfitting (0) | 2022.09.27 |
|---|---|
| Deep Learning - 3.2~3.3 Implementation of Multilayer Perceptrons (0) | 2022.09.20 |
| Deep Learning - 2.7 Concise Implementation of Softmax Regression (0) | 2022.09.01 |
| Deep Learning - 2.6 Implementation of Softmax Regression from Scratch (0) | 2022.08.23 |
| Deep Learning - 2.5 The Image Classification Dataset (0) | 2022.08.19 |



