
Now we will implement softmax regression from scratch
- Initialize Model parameters
- Defining the softmax operation
- Defining the Model
- Defining the loss funciton
1. Initialize Model Parameters
Each example in the raw dataset is a 28 × 28 image. We will flaten them into a vector of length 784 and treat each pixel location as just another feature.
Because our dataset has 10 classes, our network will have an output dimension of 10.
So out weights will constitute a 784 × 10 matrix and the biases will constitute a 1 × 10 row vector.
initialize our weights W with Gaussian noise and our biases to take the initial value 0.

2. Defining Softmax Operation
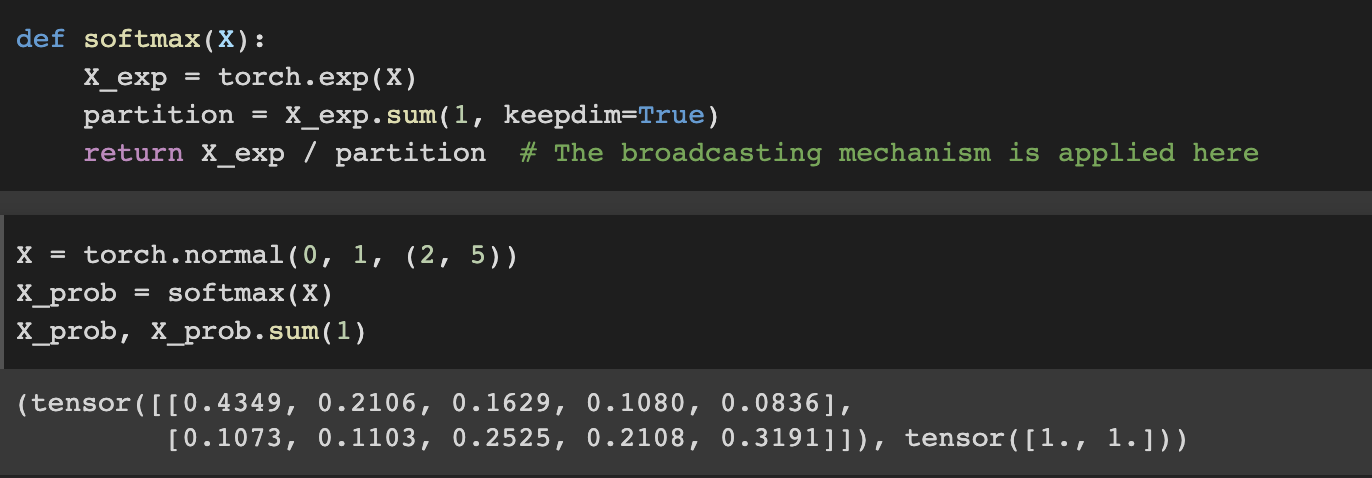
3. Defining the model

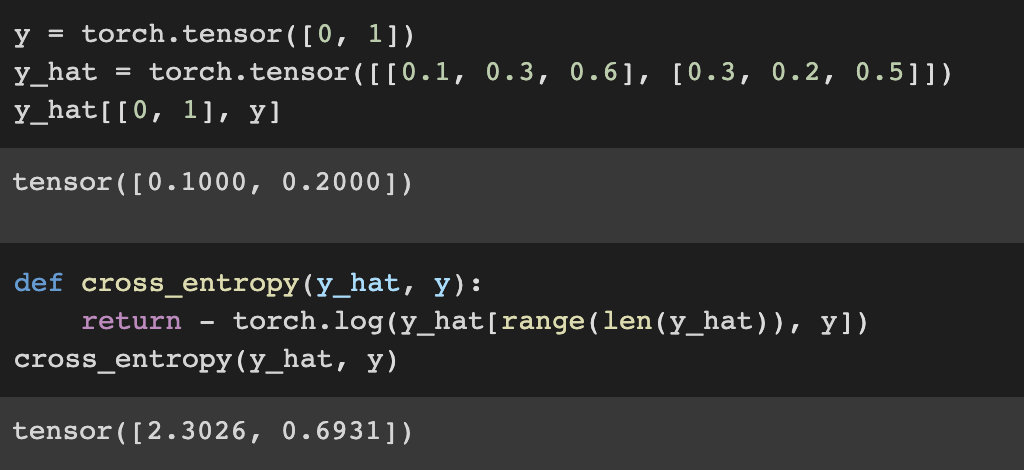
4. Defining the loss function
Instead of using for loop we can make cross-entrophy loss more efficiently.
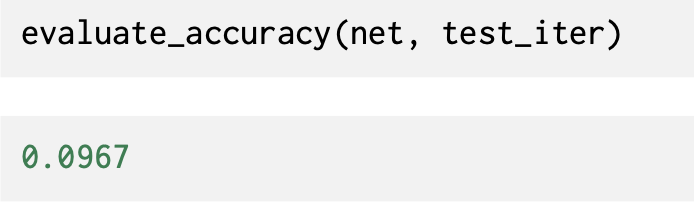
5. Classification Accuracy

The result is a tensor containing entries of 0 (false) and 1 (true). Taking the sum yields the number of correct predictions.
y_hat.argmax(axis=1) 's result is [2,2]
and y is [0,2]
so the accuracy is 0.5



6. Traning
First, we define a function to train for one epoch.
def train_epoch_ch3(net, train_iter, loss, updater):
"""The training loop defined in Chapter 3."""
# Set the model to training mode
if isinstance(net, torch.nn.Module):
net.train()
# Sum of training loss, sum of training accuracy, no. of examples
metric = Accumulator(3)
for X, y in train_iter:
# Compute gradients and update parameters
y_hat = net(X)
l = loss(y_hat, y)
if isinstance(updater, torch.optim.Optimizer):
# Using PyTorch in-built optimizer & loss criterion
updater.zero_grad()
l.mean().backward()
updater.step()
else:
# Using custom built optimizer & loss criterion
l.sum().backward()
updater(X.shape[0])
metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
# Return training loss and training accuracy
return metric[0] / metric[2], metric[1] / metric[2]
The following training function then trains a model net on a training dataset accessed via train_iter for multiple epochs, which is specified by num_epochs.
def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater): #@save
"""Train a model (defined in Chapter 3)."""
animator = Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9],
legend=['train loss', 'train acc', 'test acc'])
for epoch in range(num_epochs):
train_metrics = train_epoch_ch3(net, train_iter, loss, updater)
test_acc = evaluate_accuracy(net, test_iter)
animator.add(epoch + 1, train_metrics + (test_acc,))
train_loss, train_acc = train_metrics
assert train_loss < 0.5, train_loss
assert train_acc <= 1 and train_acc > 0.7, train_acc
assert test_acc <= 1 and test_acc > 0.7, test_accwe use the minibatch stochastic gradient descent to optimize the loss function of the model with a learning rate 0.1.
lr = 0.1
def updater(batch_size):
return d2l.sgd([W, b], lr, batch_size)Now we train the model with 10 epochs.
num_epochs = 10
train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, updater)
7. Prediction
Now that training is complete, our model is ready to classify some images.
def predict_ch3(net, test_iter, n=6): #@save
"""Predict labels (defined in Chapter 3)."""
for X, y in test_iter:
break
trues = d2l.get_fashion_mnist_labels(y)
preds = d2l.get_fashion_mnist_labels(net(X).argmax(axis=1))
titles = [true +'\n' + pred for true, pred in zip(trues, preds)]
d2l.show_images(
X[0:n].reshape((n, 28, 28)), 1, n, titles=titles[0:n])
predict_ch3(net, test_iter)'ComputerScience > Machine Learning' 카테고리의 다른 글
| Deep Learning - 3.1 Multilayer perceptrons (0) | 2022.09.15 |
|---|---|
| Deep Learning - 2.7 Concise Implementation of Softmax Regression (0) | 2022.09.01 |
| Deep Learning - 2.5 The Image Classification Dataset (0) | 2022.08.19 |
| Deep Learning - 2.4 Softmax Regression (0) | 2022.08.18 |
| Deep Learning - 2.3 Concise Implementation of Linear Regression (0) | 2022.08.16 |



