
This time we will use high-level-apis of deep learning framework to implement softmax regression.
first load mnist-fashion data
import torch
from torch import nn
import torchvision
from torchvision import transforms
from torch.utils import data
import matplotlib.pyplot as plt
import numpy
# `ToTensor` converts the image data from PIL type to 32-bit floating point
# tensors. It divides all numbers by 255 so that all pixel values are between
# 0 and 1
trans = transforms.ToTensor()
mnist_train = torchvision.datasets.FashionMNIST(
root="../data", train=True, transform=trans, download=True)
mnist_test = torchvision.datasets.FashionMNIST(
root="../data", train=False, transform=trans, download=True)
batch_size = 256
train_iter = data.DataLoader(mnist_train, batch_size, shuffle=True,
num_workers=4)
test_iter = data.DataLoader(mnist_test, batch_size, shuffle=False,
num_workers=4)- Initializing Model parameters
- Softmax Implementation revisited
1. Initializing Model parameters
To implement our model, we just need to add one fully-connected layer with 10 outputs to our Sequential
we initialize the weights at random with zero mean and standard deviation 0.01.
# PyTorch does not implicitly reshape the inputs. Thus we define the flatten
# layer to reshape the inputs before the linear layer in our network
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, std=0.01)
net.apply(init_weights);2. Softmax Implementation Revisited
To avoid exponential to be inf or nan we can do some tricks
First subtract max(ok) from all ok before proceeding with the softmax calculation.
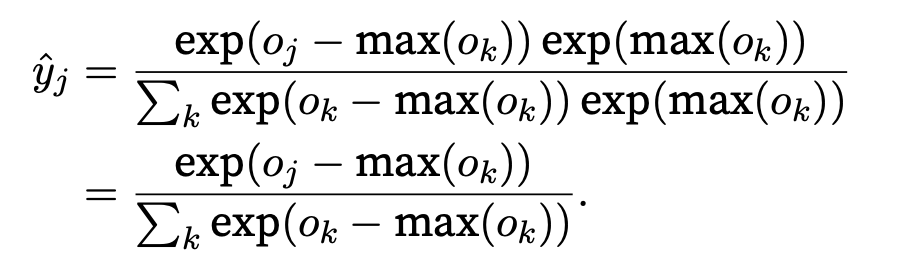
But still, these might be rounded to zero due to finite precision (i.e., underflow), making yˆj zero and giving us -inf for log(yˆj ). A few steps down the road in backpropagation, we might find ourselves faced with a screenful of the dreaded nan results.
But fortunately we ultimately intend to take their log. By combining these two operators softmax and cross-entropy together, we can escape the numerical stability issues that might otherwise plague us during backpropagation.
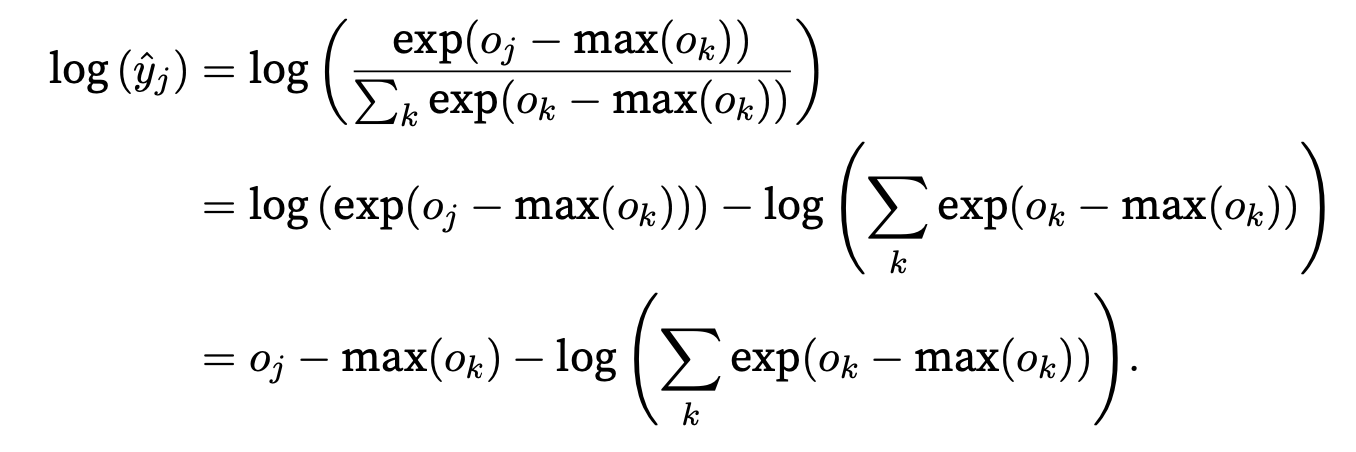
loss = nn.CrossEntropyLoss(reduction='none')We will just pass the logits and compute the softmax and its log all at once inside the cross-entropy loss function
3. Optimization Algorithm
trainer = torch.optim.SGD(net.parameters(), lr=0.1)We use minibatch stochastic gradient descent with a learning rate of 0.1 as the optimiza- tion algorithm.
4. Training
def accuracy(y_hat, y):
"""Compute the number of correct predictions."""
if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
y_hat = y_hat.argmax(axis=1)
cmp = y_hat.type(y.dtype) == y
return float(cmp.type(y.dtype).sum())
num_epochs = 10
test_accuracy = []
train_loss = []
train_accuracy = []
for epoch in range(num_epochs):
train_loss_sum = 0.0
train_acc_sum = 0
train_y_num = 0
for X, y in train_iter:
# Compute gradients and update parameters
y_hat = net(X)
l = loss(y_hat, y)
# Using PyTorch in-built optimizer & loss criterion
trainer.zero_grad()
l.mean().backward()
trainer.step()
train_loss_sum += float(l.sum())
train_acc_sum += accuracy(y_hat, y)
train_y_num += y.numel()
# evaluate train accuracy, loss
train_loss.append(train_loss_sum / train_y_num)
train_accuracy.append(train_acc_sum / train_y_num)
# evaluate test accuracy
net.eval() # Set the model to evaluation mode
test_acc = 0.0
y_num = 0.0
with torch.no_grad():
for X, y in test_iter:
test_acc += accuracy(net(X), y)
y_num += y.numel()
test_accuracy.append(test_acc / y_num)
plt.plot(test_accuracy, label='test accuracy')
plt.plot(train_accuracy, label='train accuracy')
plt.plot(train_loss, label='test loss')
plt.legend()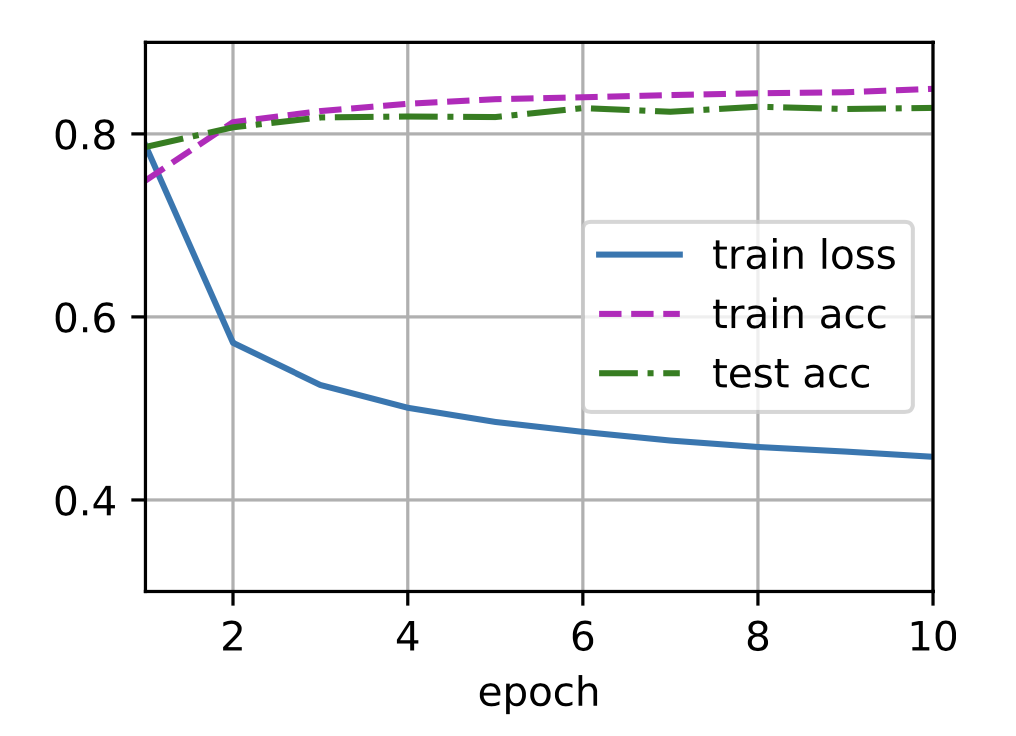
'ComputerScience > Machine Learning' 카테고리의 다른 글
| Deep Learning - 3.2~3.3 Implementation of Multilayer Perceptrons (0) | 2022.09.20 |
|---|---|
| Deep Learning - 3.1 Multilayer perceptrons (0) | 2022.09.15 |
| Deep Learning - 2.6 Implementation of Softmax Regression from Scratch (0) | 2022.08.23 |
| Deep Learning - 2.5 The Image Classification Dataset (0) | 2022.08.19 |
| Deep Learning - 2.4 Softmax Regression (0) | 2022.08.18 |



