1. edge
- 엣지는 왜 생길까? 깊이가 불연속적인 지점, surface normal 벡터와 빛이 오는 방향이 수직인 지점 등 다양한 이유로 윤곽선이 생긴다.

- 영상처리에서는 image intensity의 급격한 변화가 있는 지점을 edge로 판단한다.

- 빨간선을 따라가며 픽셀의 intensity를 조사해보면 edge부분에서 급격한 intensity차이가 보인다. 저 곡선의 derivative가 클수록 변화가 더 크다고 볼 수 있고 edge에 유력해진다.
- first derivative의 극점이 edge일 확률이 제일 높다. 근데 일차 도함수에서 극점을 찾기가 어려우니 한 번 더 미분한다. 2차 도함수에서 함수값이 0인 부분이 1차 도합수의 극점이기 때문이다. (zero crossing 포인트 찾기)
2. image gradient
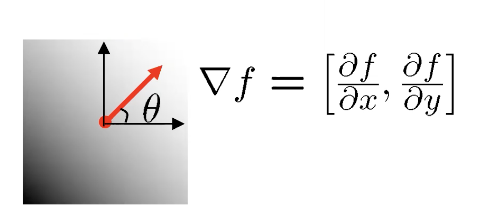
- 좀 더 확장하면 이렇게 모든 픽셀에 대해서 모든 방향을 고려한 gradient를 구할 수 있다. 그라디언트는 [x변화량, y변화량]으로 나타낸다.
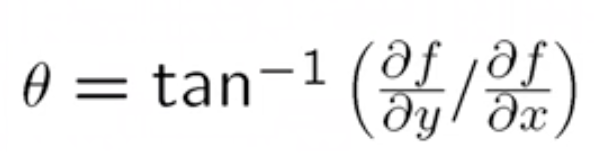

- 한 지점의 edge strength는 gradient 크기(magnitude)에 의해 결정된다.
- 방향은 탄젠트 역함수를 활용한다.
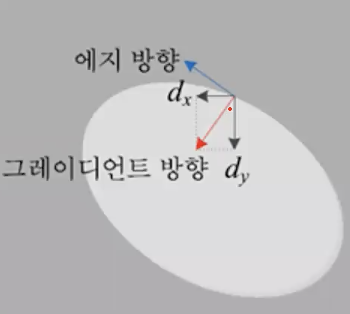
- 실제로 저 지점에서 그라디언트 방향과 크기를 화살표로 나타내면 위와 같다. 더 밝은 방향으로 화살표가 그려진다.
- 그라디언트 방향에 수직인 방향이 edge의 방향이다.
3. Differentiation & convolution
- 그럼 그라디언트는 실제로 어떻게 구할 수 있을까?
- convolution을 통해 구한다.

- 이 convolution mask를 적용하면 x 지점에서 +가로방향의 first derivative를 구할 수 있다.
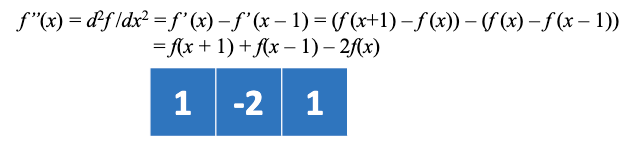
- 이 conovlution mask를 적용했을 때, x지점에서의 가로방향 second derivative를 구할 수 있다.
* 참고로 마스크에 채워진 값들을 weight라고 한다.

- 실제로 밝기값이 그림과 같은 영상이 있다고 하자. 영상 f, 1차 도함수 f', 2차 도함수 f''를 차례로 구해보았다.
- 1차 도함수의 결과를 보면 step edge는 잘 찾는데 ramp edge는 잘 찾지 못한다.
- 2차 도함수의 결과를 보면 (4, -4), (0,-1), (-1,0), (0,1), (1,0) 구간에서 zero crossing point를 찾아낸다. 즉 step, ramp edge를 모두 잘 찾아내었다.
- 2차 도함수의 결과 픽셀 값들을 보고 내가 설정한 threshold 보다 크면 에지로 결정하자! 라고 할수 있다.
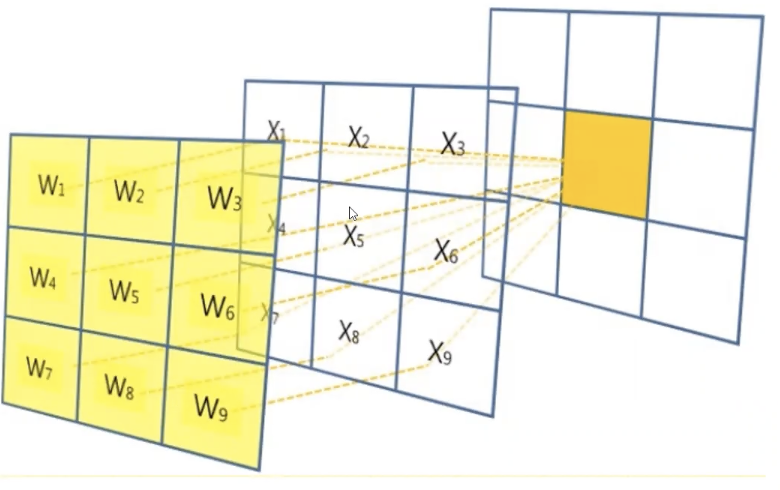
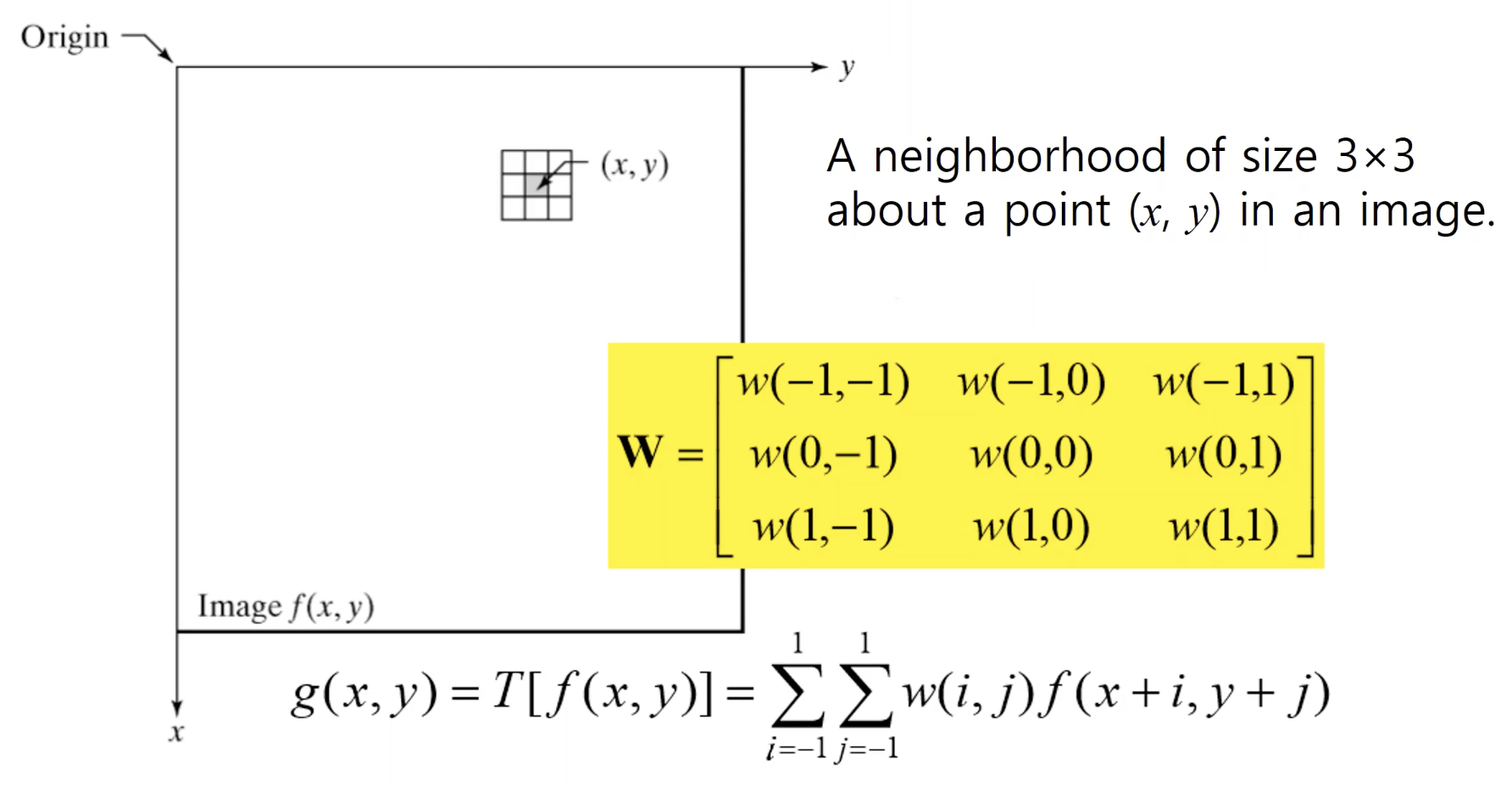
- 이차원 영상에 convolution을 수행하는 과정은 위와 같다.
- 중심점을 anchor포인트라고 한다.
3. edge model
- 이제 edge를 검출하는 모델을 살펴보자.
- 노이즈를 고려하여 에지를 찾기 위해 중앙차분으로 에지를 판단한다. 인접 픽셀말고 좀 더 넓은 간격을 고려해본다.
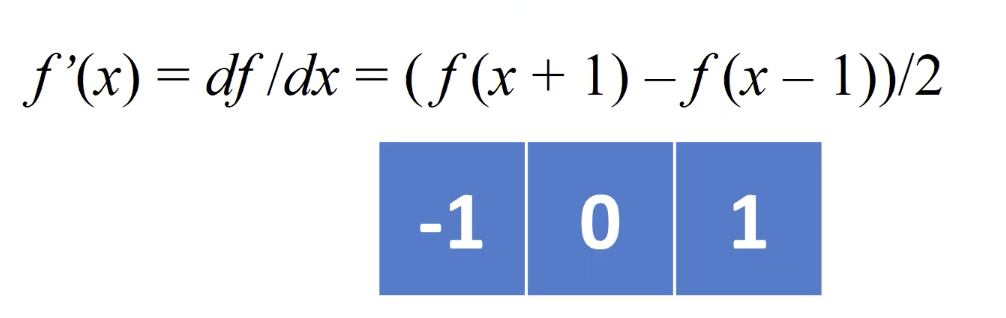


- 중앙차분, centered divided difference 으로 좀 더 안정적인 edge를 탐색한다.



- 실제로 edge검출 convolution(kernel, filter, mask)을 적용하면 edge들을 검출할 수 있다.
4. noise
- 이미지에 noise는 아주 빈번하게 존재한다. 이를 고려해서 convolution mask의 weight와 크기를 조정한다.
- noise는 기본적으로 고주파 성질을 띠기 때문에 미분결과를 취약하게 만든다.

- 이미지에 노이즈가 낀 예시이다. 빨간 라인 한줄만 떼와서 살펴보자. x는 이미지 픽셀의 좌표 f(x)는 x에서의 밝기이다.
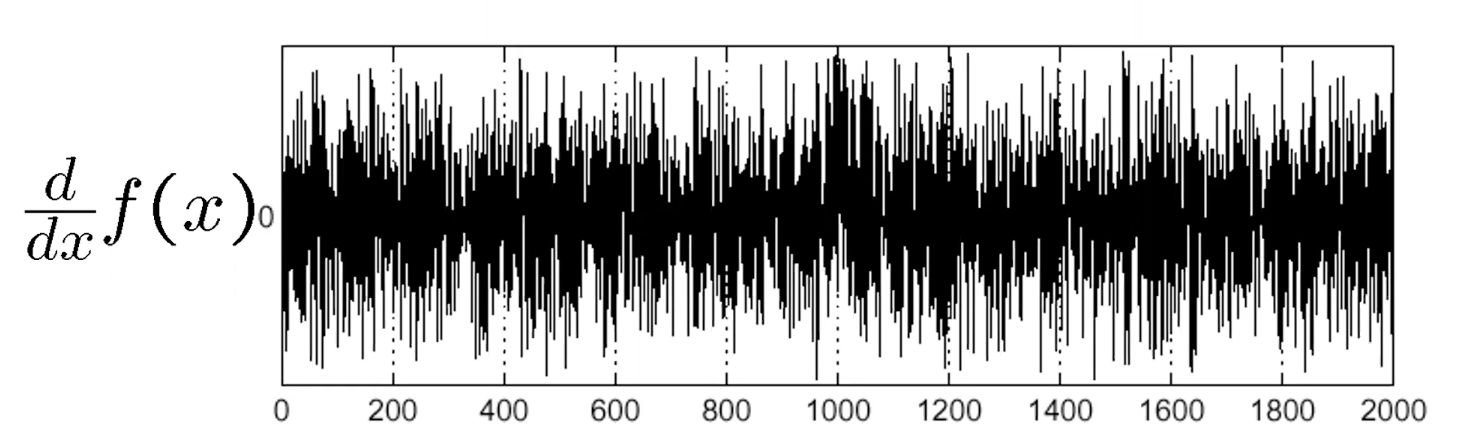
- 1차 도함수를 구한 모습이다. 도대체 누가 edge인지를 알수가 없다.
- 즉 노이즈가 많을 수록 미분필터는 영향을 크게 받을수밖에 없다.
- 우리는 derivative와 고정된 d x d 크기의 filter를 사용하기 때문에 노이즈에 특히 취약하다.

- 그래서 edge검출 전에 smoothing으로 픽셀값들의 차이를 줄이는 방법을 많이 활용한다.
- smoothing을 위한 convolution filter를 사용한다. (ex. 가우시안필터)
- smoothing때문에 영상이 살짝 선명도를 잃을 수 있지만 어쩔수 없다.
- 이렇게 총 두번의 convolution연산을 수행한다.
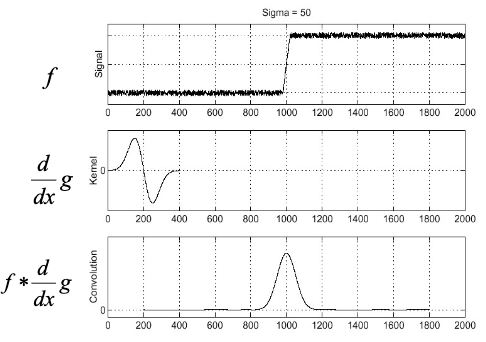
- 연산 순서를 조금바꾸면 한번의 convolution 연산만으로 결과를 구할 수 있다.
- smoothing filter(여기선 가우시안 필터)를 먼저 미분해서 만든 filter에 영상을 통과시킨다.
5. Derivative of Gaussian filter

- (좌) 가우시안 2차원 필터, (우) 미분한 가우시안 2차원 필터
- 시그마는 표준편차를 나타낸다. 구멍의 지름을 생각하면 편하다.
- 마스크가 너무 작으면 오차가 크고 너무 많으면 연산량이 커진다. 시그마에 따라 마스크 크기가 권장된다.
- 홀수를 사용하는 이유는 중심점을 기준으로 상하좌우가 대칭이 되도록 해야 하기 때문이다. (우함수를 만든다)
* 참고로 시그마 크기에 따라 검출되는 edge의 두께가 달라진다.(시그마가 클수록 세부 edge는 사라지고 큰 물체 edge 추출)
* 예를들어 시그마가 점점 커지면 얼굴의 잔주름을 잡아내다가 점점 얼굴형을 나타내는 윤곽선만 잡는다.

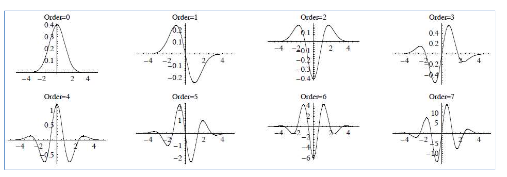
- 필터를 1차원에서 살펴보자.
- 계속해서 미분을 수행할 수 있다. 미분을 하면 할수록 zero crossing point가 더 많이 생긴다.
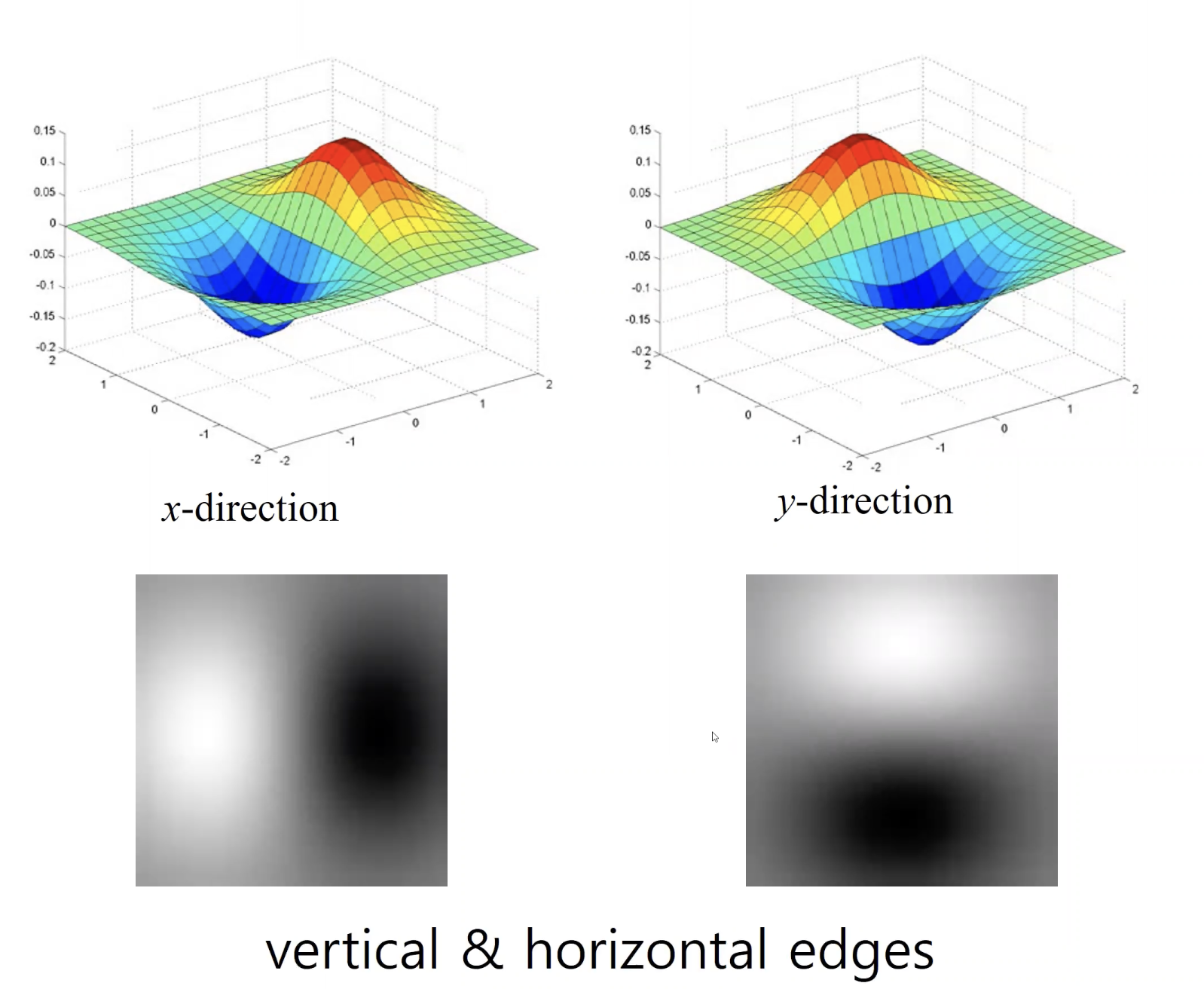
- 이 미분한 가우시안 필터를 수직, 수평으로 사용하면 vertical, horizontal edge가 검출된다.

6. Laplacian of Gaussian filter

- 2차원 마스크일 때, x, y에 대해서 각각 두번씩 미분한 것을 laplacian filtering이라고 한다. (2차 도함수)
- edge검출을 위해 사용한다.

- 하지만 현실에서는 노이즈가 상당하기 때문에 smoothing이 필요하다.
- 가우시안 필터와 라플라시안 필터링을 연달아 수행하면 연산량이 상당하기 때문에 가우시안 필터를 2차 미분한 filter를 가지고 한번만 convolution을 수행한다.
'ComputerScience > ImageProcessing' 카테고리의 다른 글
| Computer Vision - Correspondence (Template Matching) (0) | 2022.03.24 |
|---|---|
| Computer Vision - Spatial filtering (Several Filters) (0) | 2022.03.18 |
| Computer Vision - Homogenous Coordinate (0) | 2022.03.13 |
| Computer Vision - Camera Model (0) | 2022.03.03 |
| 영상처리 - 11. Histogram matching(Specification) (0) | 2021.11.11 |



