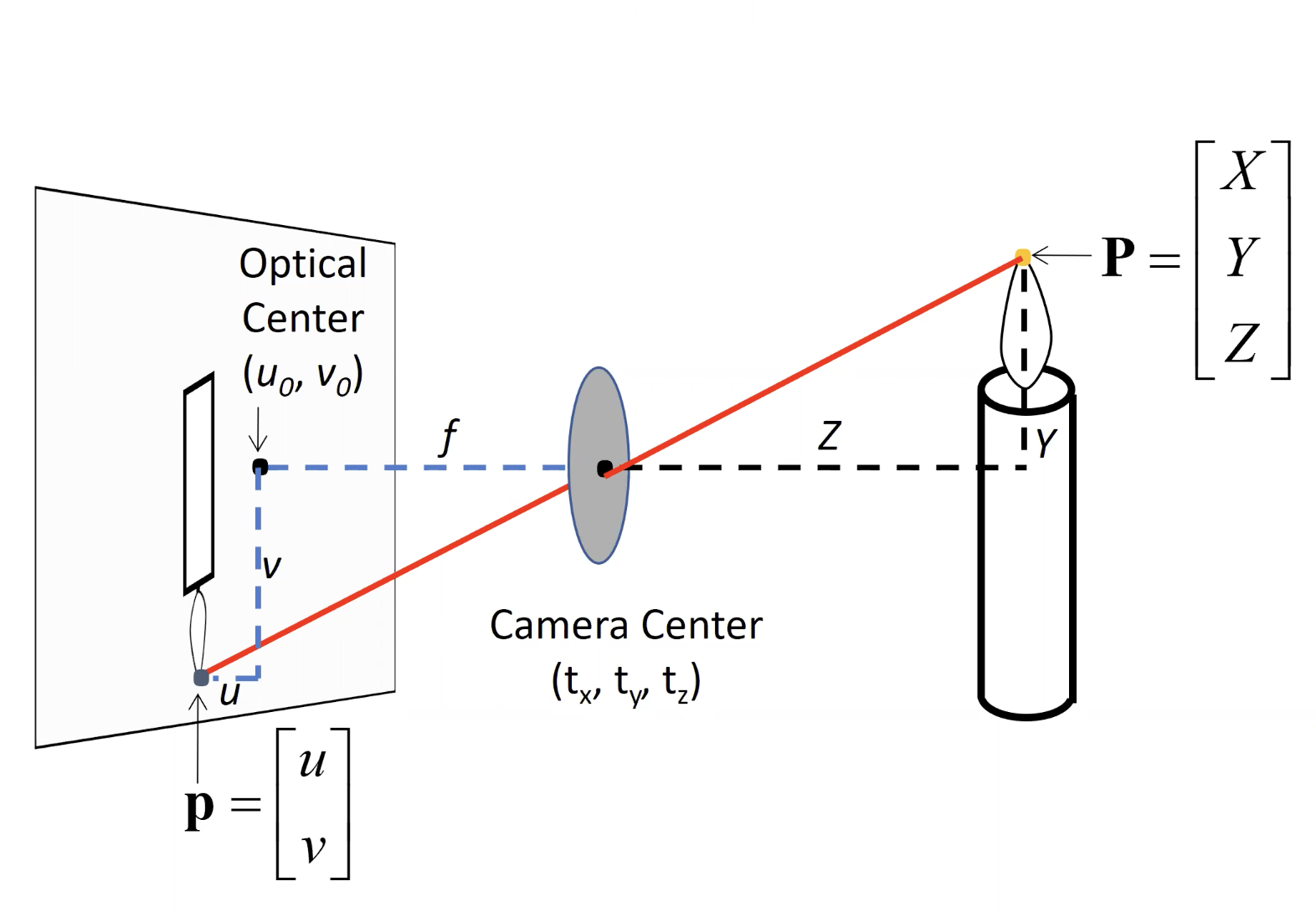
- 3차원 물체를 2D로 사영시킬때 차원이 축소된다. 카메라 좌표를 옮길때마다 3차원 물체를 다각도에서 2D화면으로 투영시킬 수 있다.
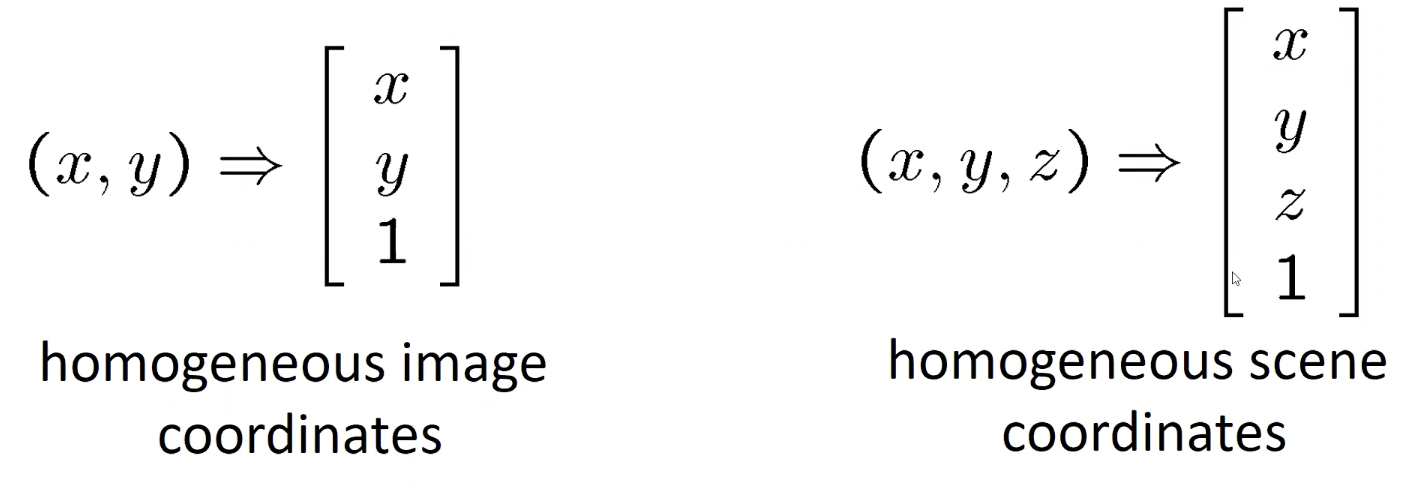
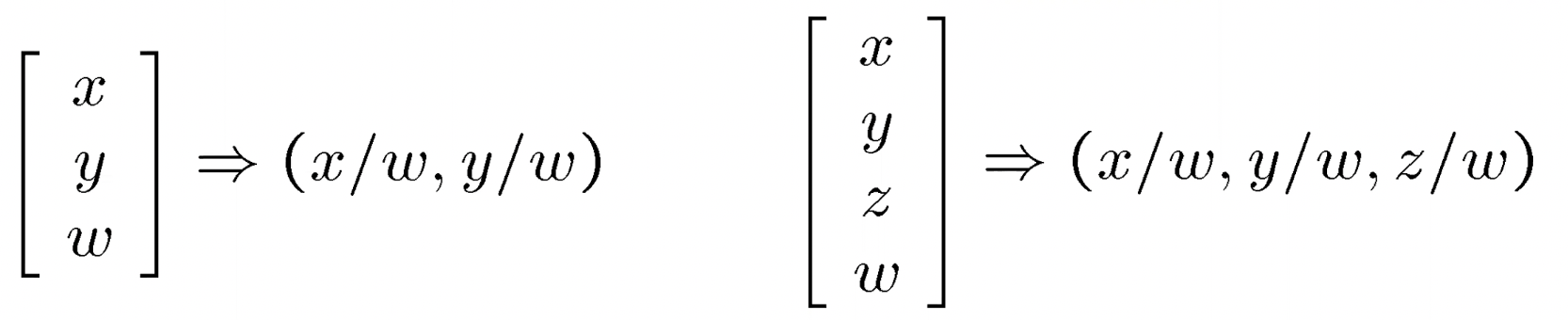
- conversion을 할때 우리는 homogeneous coordinates를 사용한다.
- 즉 동차좌표계에서 (x,y)는 (x,y,1), (2x, 2y, 2)랑 동일하다. (한 점으로 대응 되는것이 아니라 직선으로 대응)
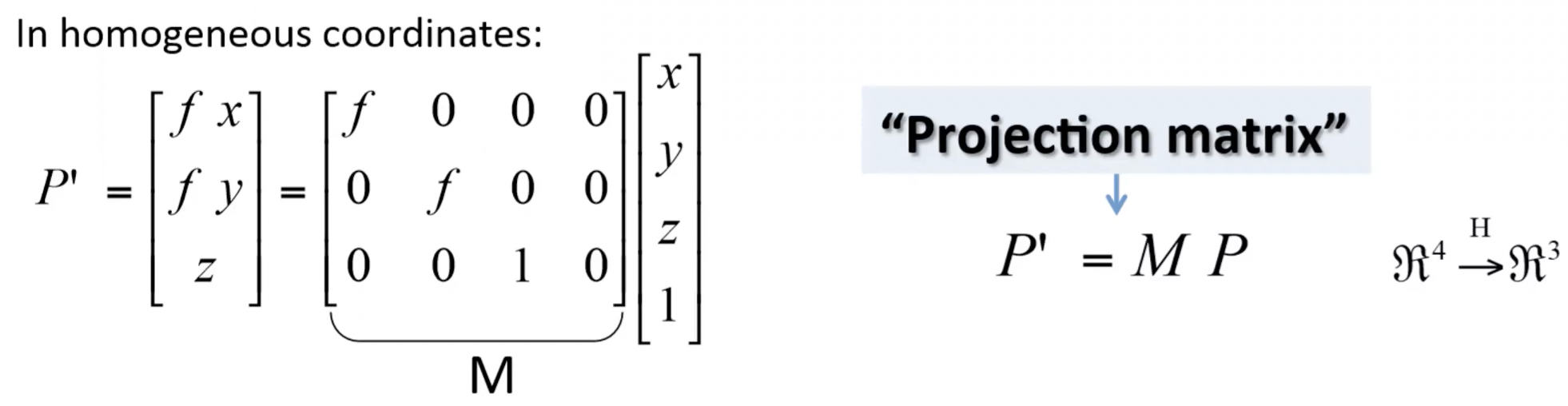
- 이렇게 Homogeneous coordinate를 도입하면 행렬의 곱셈만으로 3차원 물체를 transform, 2D화면에 투영시킬 수 있다.
- 즉 위의 예시에서는 실세계의 삼차원 좌표 (x,y,z)를 (fx/z, fy/z) 점으로 사영시켰다.
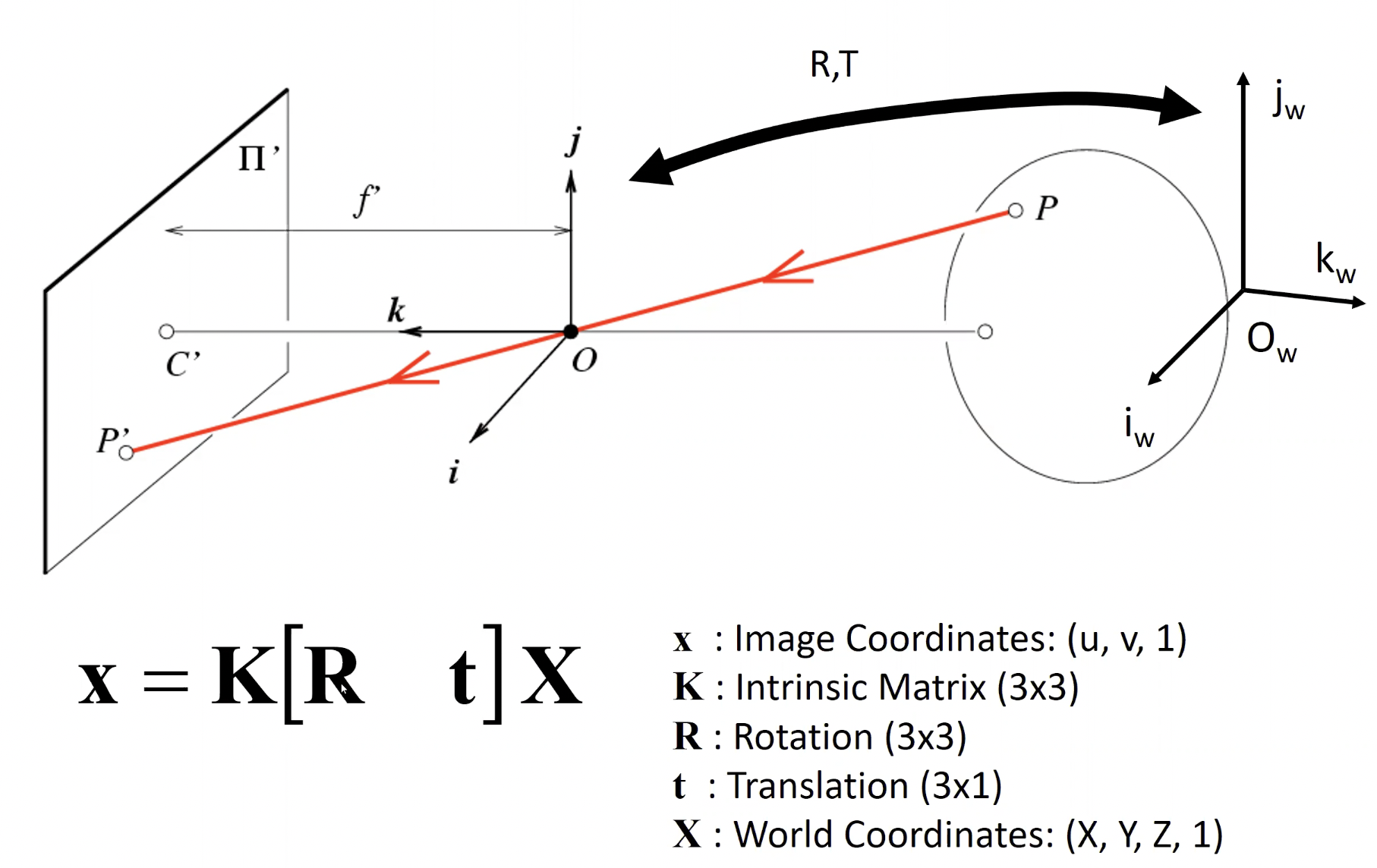
- 3차원 물체의 projection은 위와 같이 표현된다. 아래 예시를 보면 쉽게 이해할수 있다.

- Rotation을 수행하지 않는다면 R은 I가 된다. 마찬가지로 tranlation도 없다면 0이다. 이 두 행렬을 붙여서 M이 만들어진다.
- M을 수행한 결과는 카메라가 (0,0,0)에 있다고 가정한 결과이다. 즉 2D이미지의 중심도 (0,0)인 경우로 생각한다.
- 따라서 이 결과를 우리 2D화면에 맞게 변환하기 위해 intrinsic assumption이 필요하다.
- 사영할 2D이미지의 중심이 0,0이 아니고 u, v일때,
- 2d 화면의 가로세로 비율이 a,b일때,
- 화면의 skew정도 s일때,
- 최종 변환행렬은 위와 같다.
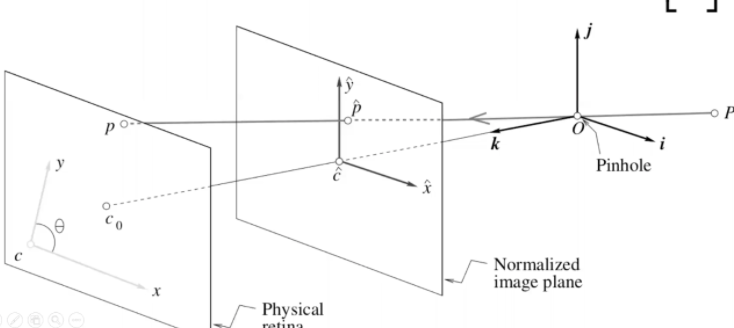
- 이렇게 1)사영을 거친후 2)실제 2D레티나에 맞게 변환이 이루어진다.

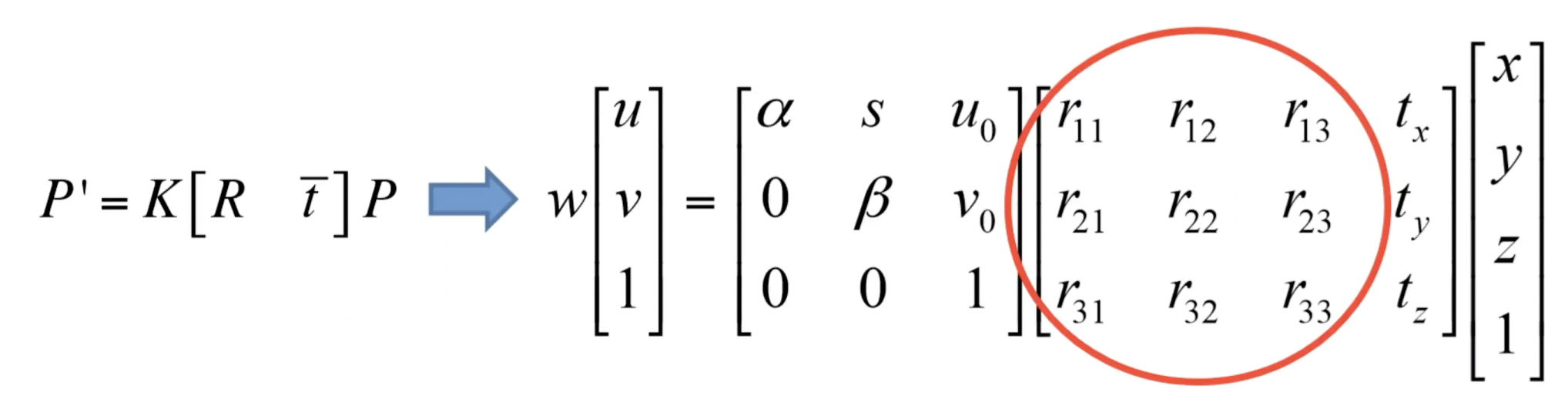
- 이번에는 intrinsic assumption과 더불어 extrinsic assumption도 있는 경우를 나타내었다.
- 카메라가 이동한 만큼 (tx,ty,tz)만큼의 변환이 수행되고 Rotation도 수행된다면 최종 변화 행렬은 위처럼 나타낼 수 있다.
- 즉 이렇게 어떤 삼차원 물체의 변환도 (u, v)로 2d화면에 사영시킬 수 있다.
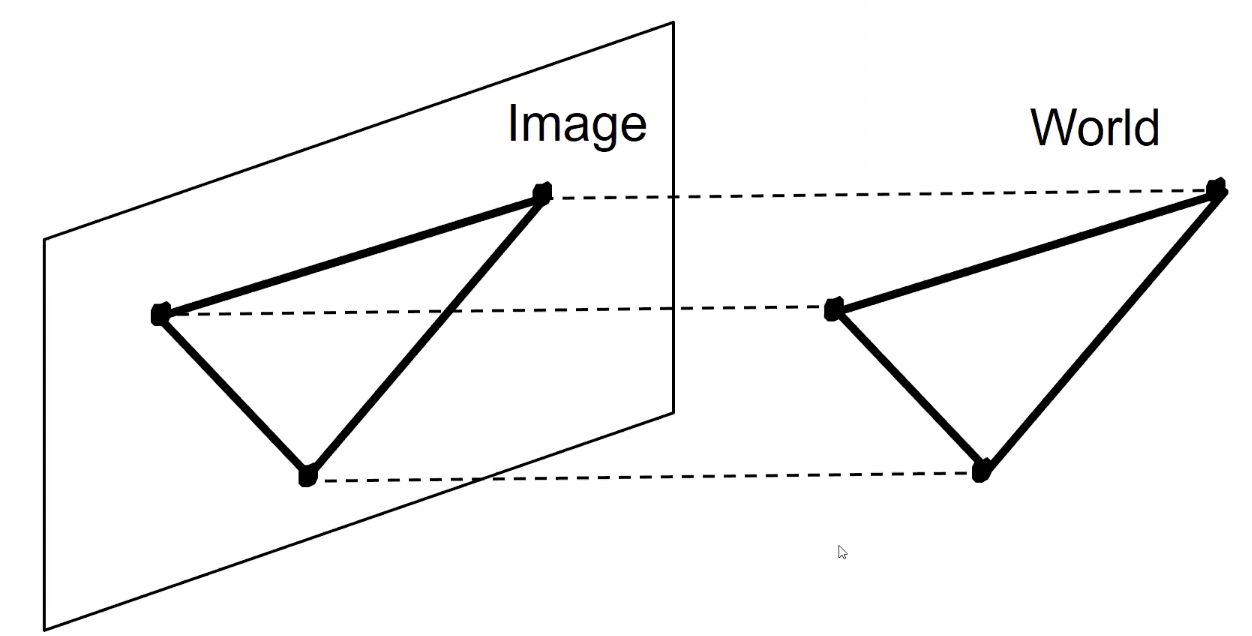
- 이제까지는 한 점을 기준으로 3차원 물체를 사영시켰다.
*라이다 센서는 점을 쏴서 공간을 스캔한다. 즉 0차원(점) ->1차원(선) -> 2차원(면) -> 3차원(공간) 복구를 수행한다.
- 이번에는 3차원 물체를 2D로 '정'사영(Orthographic projection) 시키는 변환을 알아보자.
- 즉 z로 나누지 않음으로써 실제 크기를 보존하는 것이다.
- ray들이 optical 축과 평행할때 결과를 보여준다.
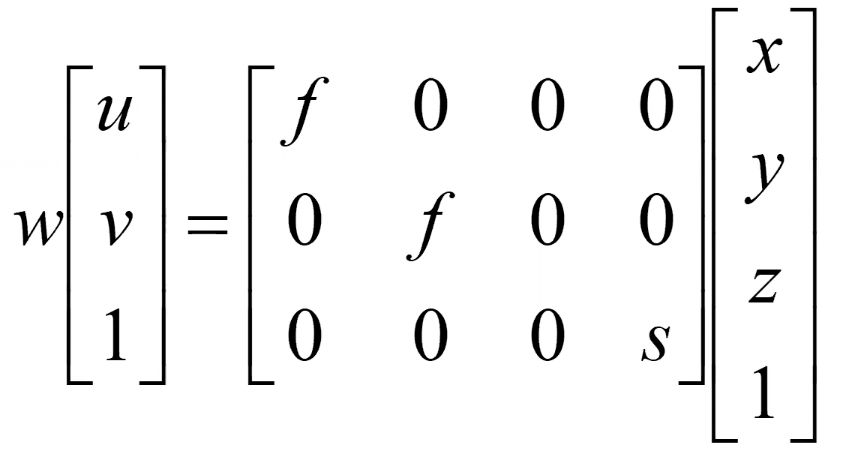
- 정사영의 projection matrix는 위와 같다. 아예 z축 값을 날려버렸다. 평면으로부터 거리만 s로 고려한다.
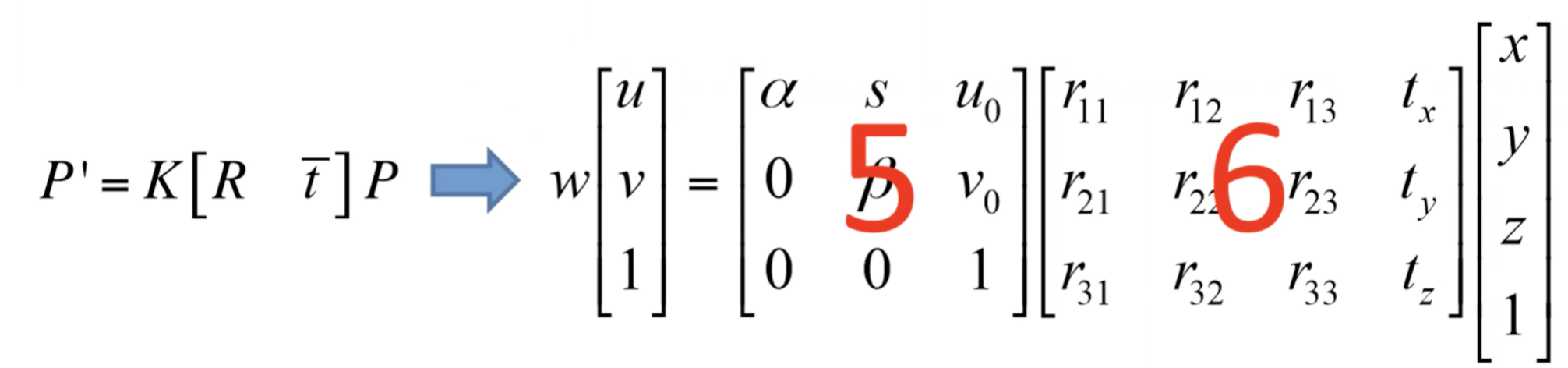
- 카메라는 3차원 물체를 2차원 이미지 센서에 담는다. 이때 만들어지는 2D이미지는 사용된 렌즈, 렌즈와 이미지 센서와의 거리, 렌즈와 이미지 센서가 이루는 각 등 카메라의 내부 파라미터에 영향을 받는다. 따라서 3차원 점들이 영상에 투영된 위치를 구하거나 역으로 영상좌표로부터 3차원 공간좌표를 복원할 때 내부 파라미터 값이 필요해진다.
- 복습) 실제 3차원 좌표는 11개의 파라미터 값에 의해 2차원 화면에 대응된다. 예를들면 드론이 11개의 파라미터 값을 알기 때문에 2차원 영상을 가지고 3차원 실제 위치를 파악할 수 있다.
- 정리하면 각각 내부, 외부 파라미터를 찾아서 카메라와 물체, 레티나의 관계를 보정하는 작업을 calibration이라고 하고 이것은 그래픽스, ar, 드론 등 많은 곳에서 사용된다.
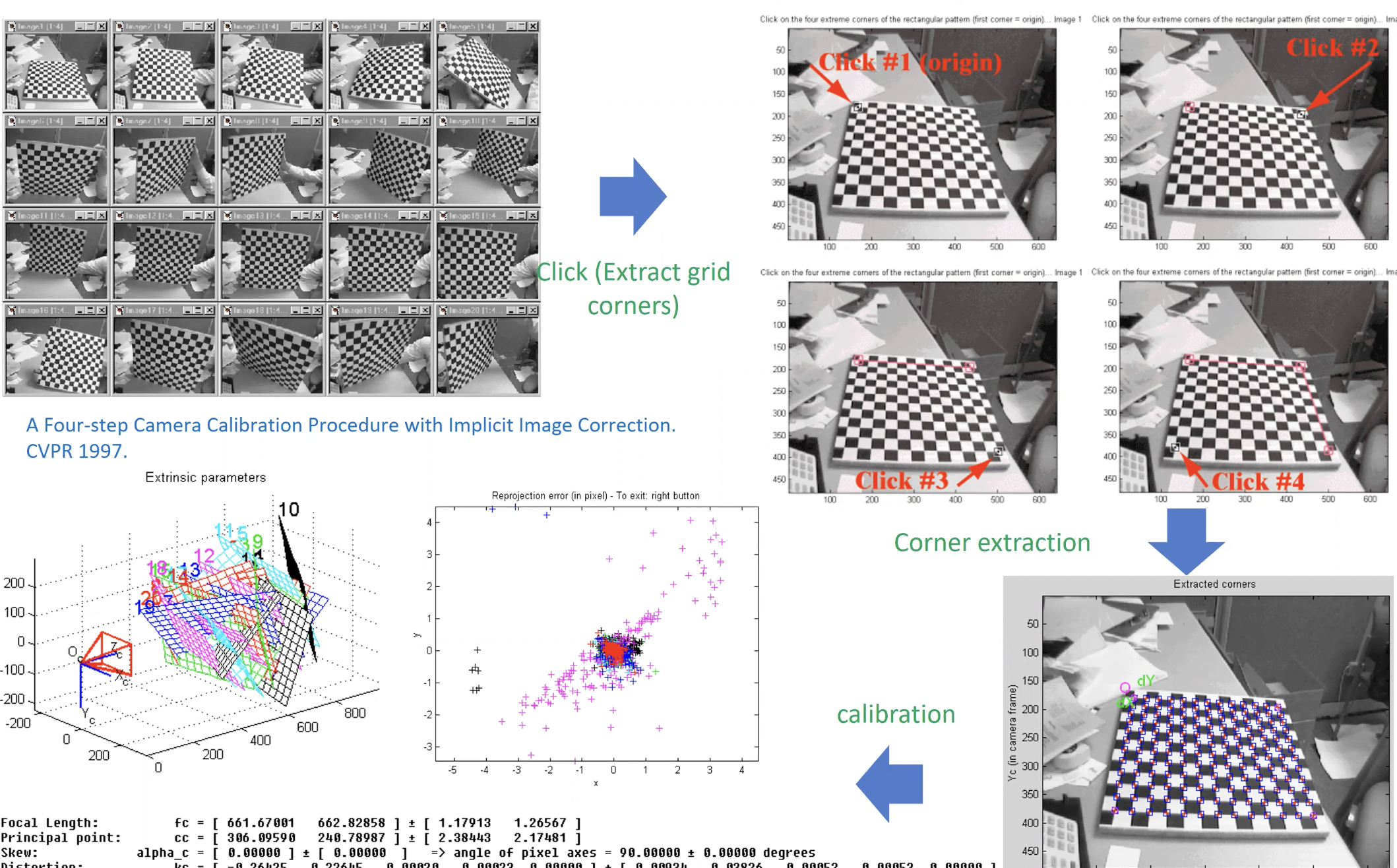
- 카메라 내부파라미터 값을 찾는데 도움을 주는 calibration toolbox이다.
- 여러 각도에서 저 체스판을 찍는다.
- 체스판 한 칸의 길이를 알고 있기 때문에 사실상 3차원 공간에서 저 체스판의 모든 꼭지점의 좌표를 알 수 있다.
- 사진을 찍었으니 2D에서 사영된 꼭지점의 좌표들도 다 알고 있다.
- 이 3D좌표들을 Projection matrix에 넣어서 이미 알고 있는 2D 좌표들과 맞는지 검사한다. 이 과정을 reprojection이라고 한다.
- 그럼 3D좌표를 Projection matrix에 넣어서 나온 2D결과, 이미 우리가 알고 있는 2D결과를 비교해서 오차가 제일 적은 Projection matrix를 구하면 카메라의 내부 파라미터 값을 구할 수 있다.
'ComputerScience > ImageProcessing' 카테고리의 다른 글
| Computer Vision - Spatial filtering (Several Filters) (0) | 2022.03.18 |
|---|---|
| Computer Vision - Spatial filtering (Convolution) (0) | 2022.03.18 |
| Computer Vision - Camera Model (0) | 2022.03.03 |
| 영상처리 - 11. Histogram matching(Specification) (0) | 2021.11.11 |
| 영상처리 - 10. Histogram Equealization (0) | 2021.11.11 |



