1. Linear Regression
- 회기란 데이터들을 2차원 공간에 찍은 후 이들을 가장 잘 설명하는 직선이나 곡선을 찾는 문제라고 생각하면 된다.
- f(x)를 fitting하는 것을 말한다. 선형의 경우 Linear, 비선형일 경우 non-linear등으로 부르기도 한다.
- 입력값이 연속된 실수이고 출력값도 연속된 실수의 경우 활용이 쉽다.
- 데이터의 경향이 fitting이 가능한 경우에 활용이 가능한 방법이다.
- 예를 들면 부모의 키에 따른 자녀의 키, 면적에 따른 주택의 가격, 연령에 따른 실업률 등이 linear regression 문제에 해당한다.

- 선형 함수를 예측할때 f(x) = Wx + b라고 하면 w를 가중치, b를 bias라고 한다. 결국은 선형 방정식을 찾는 것이다.
2. loss function
- 그럼 어떤 함수가 제일 적합하다고 판단할 수 있을까?
- 그때 사용하는 것이 loss 함수이다.

- 실제 값과 f(x)와의 차이를 활용해서 구한다.
- 이 차이들이 최소가 되는 지점이 최적화한 곳이라고 생각하면 된다.

- 즉 loss는 모든 점들에 대해서 수직 거리의 제곱의 평균으로 산출된다.
- argmin W,b는 loss를 최소로 만드는 값이 w,b라는 뜻의 표기법이다.
* 참고로 loss는 다양한 종류가 존재한다. 위에서 처럼 단순히 수치적인 차이로 loss를 구현할 수도 있지만 단순히 차이 이상의 조건으로 loss가 정의될 수 있다. 예를들어 암환자가 정상인으로 인식되는 risk를 매우 중요하게 생각한다면 risk를 최소화 하기 위해서 아래 그림처럼 직선과 점의 거리를 구하는 방식이 바뀔수도 있다.

3. Minimizing(optimizing)
- 그럼 loss를 어떻게 minimize할 수 있을까?
- 가장 많이 사용되는 방법은 gradient descent라는 경사하강법이다.

- 그래프에서 한점에서의 기울기가 0에 가까울때 까지 계속해서 그래프를 타고 내려가는 방법이다.

- 우리가 정한 loss function을 w와 b에 대해서 미분한 다음 learning rate(0.01)만큼 그 기울기를 타고 w, b값을 계속해서 갱신하는 방법이다.
- learning rate는 실험적으로 결정되는 경우가 많고 학습의 속도를 결정하는 parameter이다. 값이 크면 더 빠르게 경사를 내려가게 될 것이고 값이 너무 작다면 최적화하는데 시간이 오래걸릴 수 있다.
4. Overfitting, Underfitting
- 아래 그림을 보면 우리가 구하고자 하는 함수는 9차함수로 주어진 데이터에 대해 완벽하게 fitting이 되어있다.
- 하지만 이런 경우는 막상 실세계의 다른 (학습때 보지못한) 데이터들을 전부 비껴갈 위험이 있다.
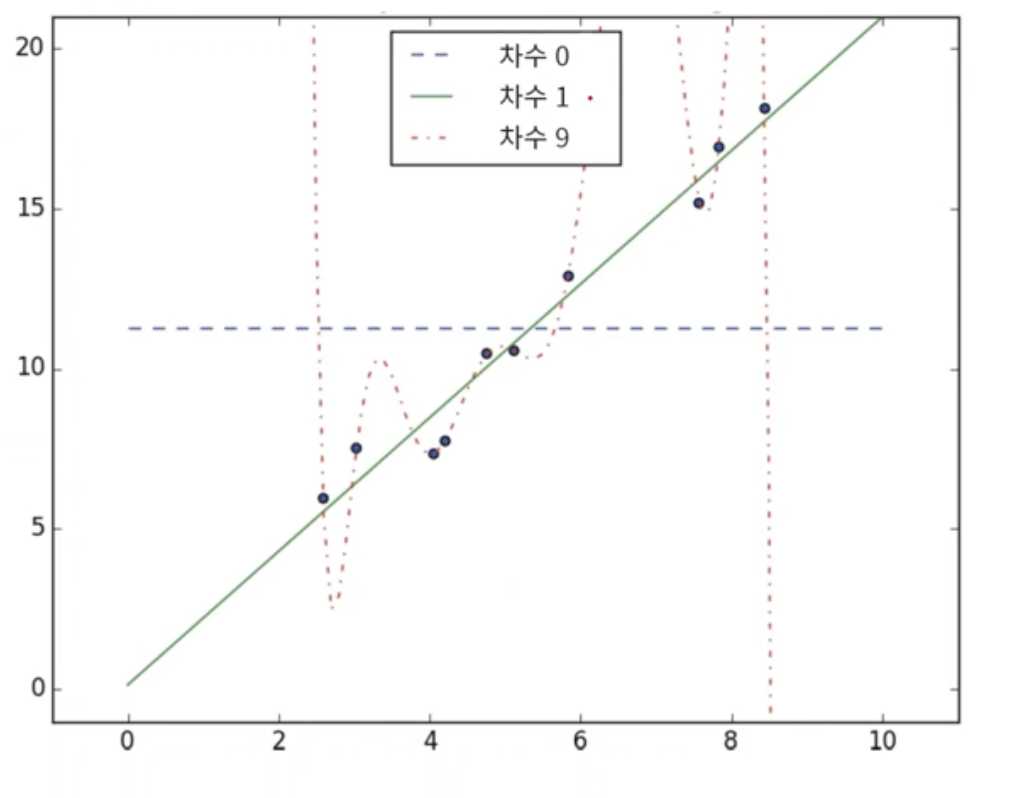
- 반대로 underfitting이라면 아예 모델 자체가 학습데이터 조차 fitting을 못 하고 있는 것이다.
'ComputerScience > Machine Learning' 카테고리의 다른 글
| AI - 10. Perceptron (0) | 2021.11.18 |
|---|---|
| AI - 9. kNN, Gaussian Mixture (0) | 2021.11.11 |
| AI - 7. 머신러닝 개요 (0) | 2021.11.03 |
| AI - 6. Uncertainty (0) | 2021.10.12 |
| DeepLearning 2-2-1 (0) | 2021.10.06 |



