1. Dynamic Programming
- 크고 어려운 문제가 있으면 잘게 나누어서 처리하되 한번 푼 문제는 다시 풀지 않음
- 이미 계산한 결과는 배열에 저장하고 필요시 다시 계산하는 것이 아니라 활용
- 이런 과정을 Memoization이라고 한다.
- DP를 적용하려면 대게 두가지 조건이 충족되어야 한다.
1. 큰 문제를 작은 문제로 나눌 수 있다.
2. 작은 문제의 정답은 그것을 포함하는 큰 문제에서도 동일하다.
- 즉 여러개의 하위 문제로 나누어 푼 다음, 그것을 결합하여 최종 목적에 도달하는 방식이다.
2. 백준 9461번
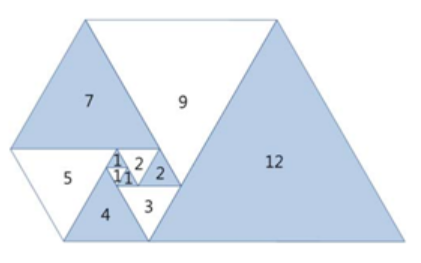
- n번째 삼각형의 변의 길이를 구해야한다.
- 먼저 정답을 도출하기 위한 점화식을 구한다.

- 이 점화식을 재귀로 풀면 다음과 같다. 동일한 값을 구하기 위해 같은 연산을 반복하는 문제가 생긴다.

반복을 피하기 위해 dynamic programming으로 문제를 해결해보자.
class Triangle
{
private:
vector<long> list;
int c;
public:
Triangle():c(5)
{
list.push_back(0);
list.push_back(1);
list.push_back(1);
list.push_back(1);
list.push_back(2);
list.push_back(2);
}
void nth(int n)
{
if(c>=n)
cout<<list[n]<<'\n';
else
{
while(c<n)
{
list.push_back(list[c]+list[c-4]);
c++;
}
c=n;
cout<<list[c]<<'\n';
}
}
};- list : 이전의 계산 결과들을 저장할 공간
- c : 초기 값으로 5번째 삼각형의 변의 길이까지는 알고 있다.
- 13~18 : 초기값 설정
- 23~24 : 1 <= n <= 5 일때
- 27~33 : 5 <= n 일때, 점화식을 계산하고 중간 결과들을 저장
2. 백준 11053번
- 가장 긴 증가하는 부분 수열 길이 구하기 (Longest Increasing Sequence)

void LIS()
{
for(int i =0; i<n;i++)
{
cin>>number[i];
for(int j = i-1; j>=0; j--)
{
if(number[i]>number[j])
{
if(len[i]<len[j]+1)
len[i] = len[j]+1;
}
}
}- 28 : i(새로운 수열의 끝)가 j(이전 수열의 끝)보다 커야 뒤에 붙을 수 있고
- 29 : j(이전 수열의 길이)가 최대여야 i(새로운 수열의 길이)도 최대가 될 수 있으므로 28번 줄의 조건을 만족하는 후보 중 길이가 가장 긴 수열을 선택한다.
3. 백준 9251번
- LCS(Longest Common Sequence, 최장 공통 부분 수열)은 두 수열이 주어졌을 때 모두의 부분 수열이 되는 수열 중 가장 긴 것이다.
- ACAYKP와 CAPCAK의 LCS는 ACAK로 길이는 4이다.
void LCS(string& s1, string& s2)
{
int ** a;
a = new int*[2];
for(int i =0; i<2;i++)
a[i] = new int[s2.length()+1];
for(int i=0; i<=s2.length();i++)
a[0][i]=0;
for(int i=0; i<s1.length();i++)
{
for(int j=0; j<s2.length();j++)
{
a[(i+1)%2][0]=0;
if(s1[i]==s2[j])
a[(i+1)%2][j+1]=a[i%2][j]+1;
else
a[(i+1)%2][j+1]=max(a[i%2][j+1],a[(i+1)%2][j]);
}
}
cout<<a[s1.length()%2][s2.length()];
for(int i = 0; i<2;i++)
delete []a[i];
delete []a;
}
3. 백준 12865번

void Knapsack(int n, int limit, int** obj)
{
int** dp = new int*[n];
for(int i =0; i<n; i++)
dp[i]=new int[limit+1];
for(int i=0; i<=limit; i++)
{
if(obj[0][W]<=i)
dp[0][i]=obj[0][V];
else
dp[0][i]=0;
}
for(int i=0; i<n; i++)
dp[i][0]=0;
for(int i =1; i<n; i++)
{
for(int j=1; j<=limit; j++)
{
if(obj[i][W]<=j)
dp[i][j] = max(obj[i][V]+dp[i-1][j-obj[i][W]], dp[i-1][j]);
else
dp[i][j]=dp[i-1][j];
}
}
cout<<dp[n-1][limit];
for(int i =0; i<n;i++)
delete []dp[i];
delete []dp;
}- 생각을 조금만 더 해보면 메모리 및 코드를 줄일 수 있는 여지가 보인다.

vector<int> w;
vector<int> v;
vector<int> dp;
int main()
{
int weight,value, n, limit;
cin>>n>>limit;
for(int i =0; i<n; i++)
{
cin>>weight>>value;
w.push_back(weight);
v.push_back(value);
}
for(int i =0; i<=limit; i++)
dp.push_back(0);
for(int i =0; i<n; i++)
{
for(int j =limit; j>0; j--)
{
if(j>= w[i])
dp[j]=max(dp[j],v[i]+dp[j-w[i]]);
}
}
cout<<dp[limit];
}
'ComputerScience > Algorithm & Data Structure' 카테고리의 다른 글
| Algorithm&DataStructure - Dijkstra (0) | 2022.01.04 |
|---|---|
| Algorithm&DataStructure - Queue (0) | 2021.08.31 |
| Algorithm&DataStructure - BFS (0) | 2021.08.02 |
| Algorithm&DataStructure - DFS (0) | 2021.08.02 |
| Algorithm&DataStructure - Divide and Conquer (0) | 2021.07.26 |



