1. Dijkstra
- 간선에 가중치가 있는 그래프에서 시작 노드가 주어졌을때 시작 노드로부터 각 노드까지의 최단 경로를 찾는 알고리즘이다.
- 참고 : https://blog.naver.com/ndb796/221234424646
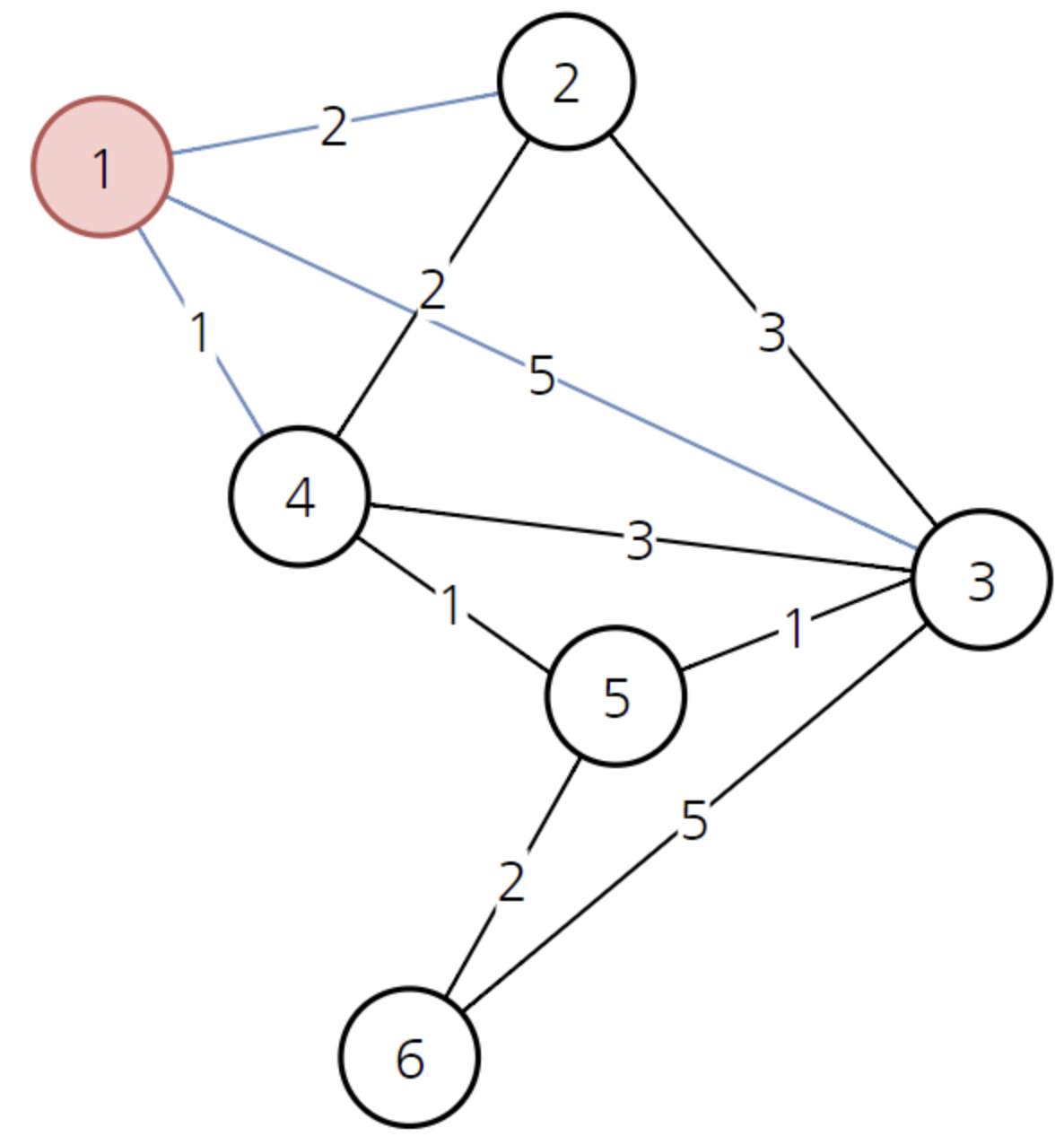

- 1번 노드의 비용이 가장 작기 때문에 1번 부터 시작해서 갈 수 있는 노드들의 비용을 갱신한다.


- 1번을 제외하고 노드중에 비용이 가장 작은것은 4번이다.
- 4번을 경유했을 때, 나머지 2, 3, 5, 6번 노드의 비용을 갱신한다.


- 1, 4 번을 제외하고 남은 노드 중 비용이 가장 적은 것은 2번이다.
- 2번을 경유해서 3, 5, 6번으로 가는 최소 비용을 갱신한다.
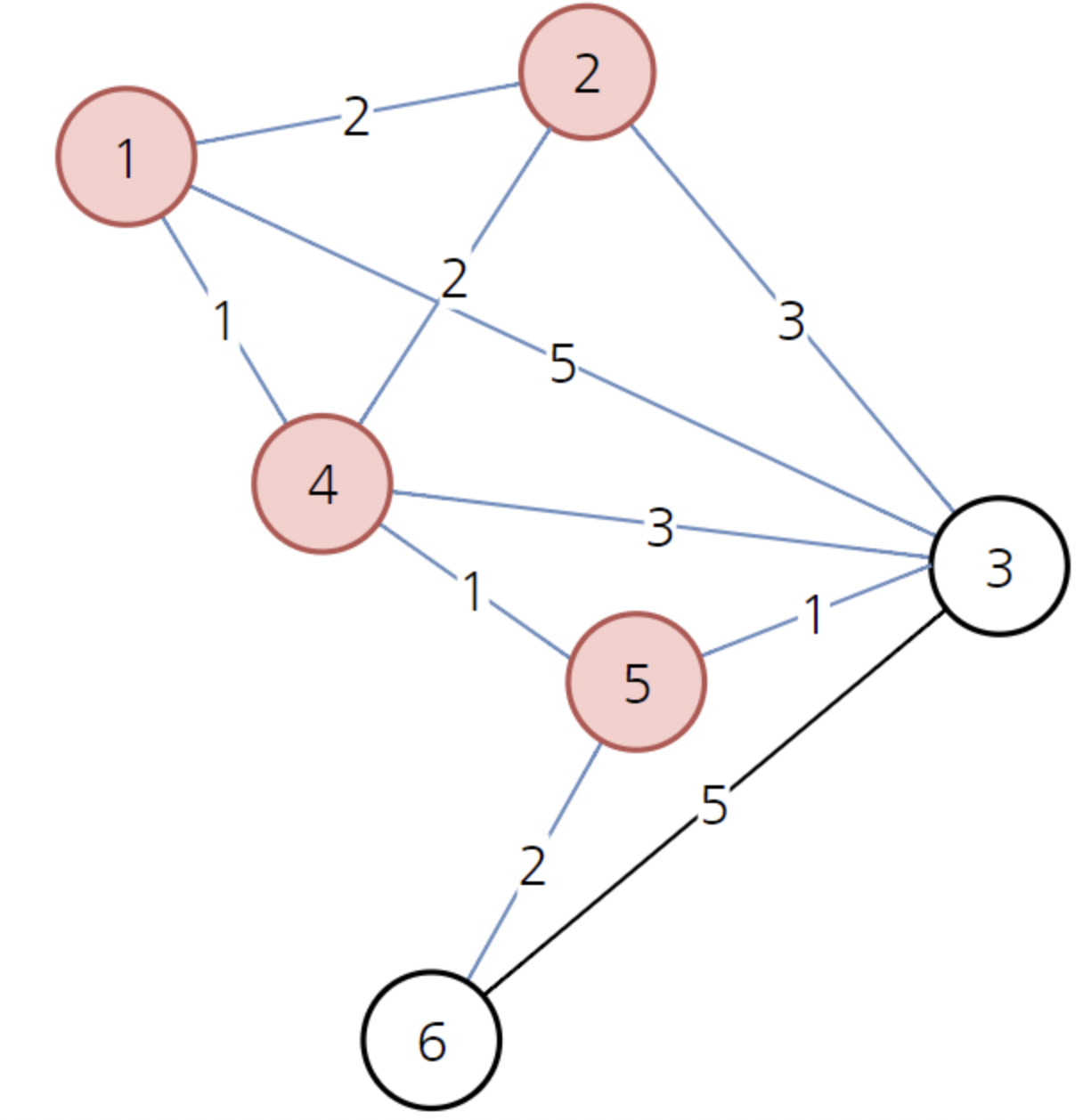

- 1, 2, 4 번을 제외하고 3, 5, 6 중에 최소 비용은 5번이다.
- 5번을 경유해서 나머지 3, 6으로 가는 최소 비용을 갱신한다.
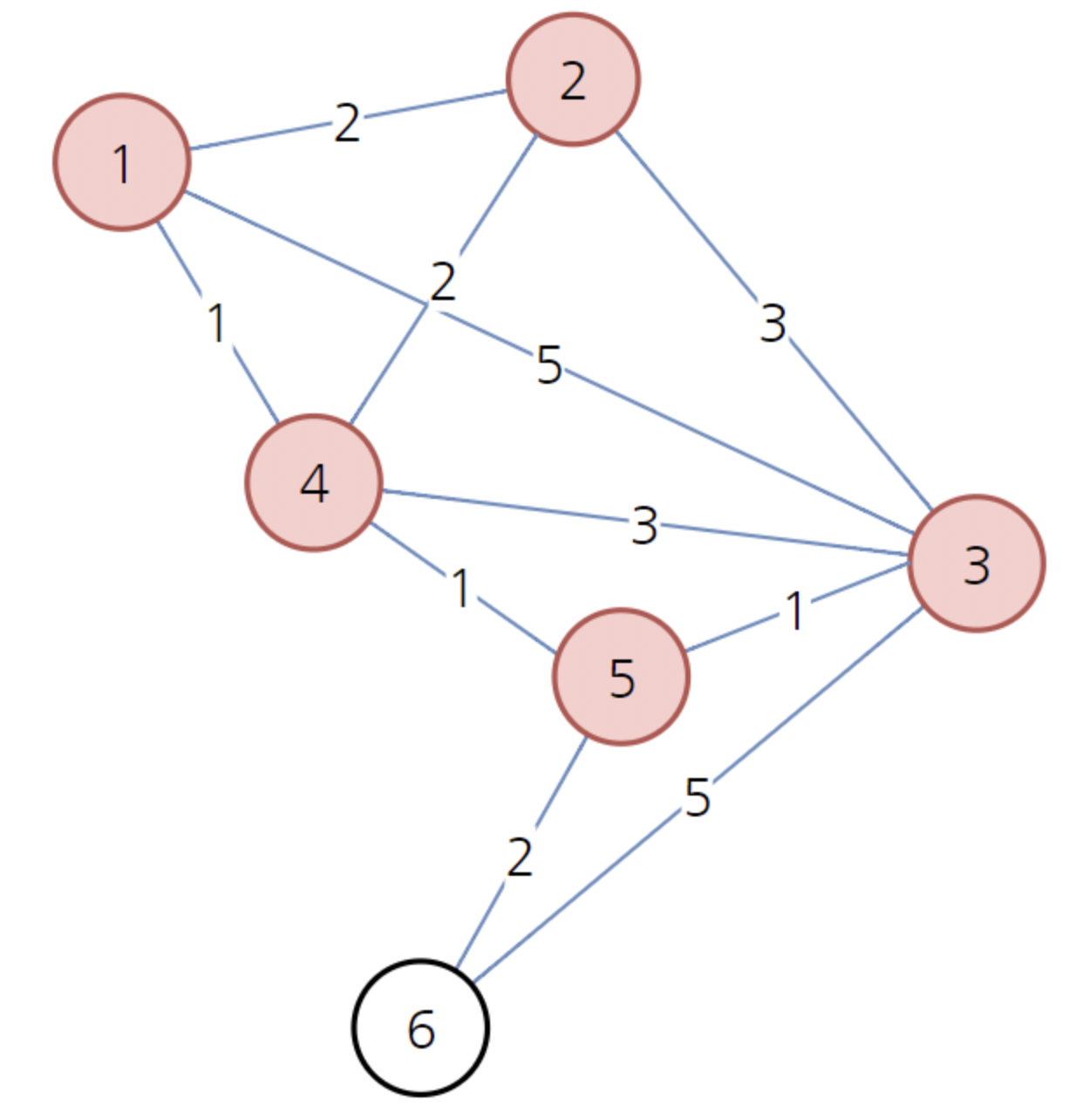

- 3, 6 번중에 최소비용은 3번이다.
- 3번을 기준으로 남아 있는(방문하지 않은) 노드의 최소비용을 갱신한다.


- 이제 남은 노드는 6번 밖에 없다.
- 6번을 경유해서 갱신할 노드가 없으니 종료된다.
2. 백준 1753번
- 방향그래프가 주어지면 주어진 시작점에서 다른 모든 정점으로의 최단 경로를 구하는 프로그램을 작성하시오. 단, 모든 간선의 가중치는 10 이하의 자연수이다.
#include <iostream>
#include <vector>
#include <queue>
#define INF 987654321
using namespace std;
int main() {
int v, e, startNode;
cin>>v>>e>>startNode;
// to, weight
vector<vector<pair<int,int>>> adj(e);
for (int i = 0; i<e; i++) {
int from,to,c;
scanf("%d %d %d", &from, &to, &c);
adj[from].push_back(make_pair(to, c));
}
// <weight, nodeNum>
priority_queue<pair<int,int>> cost;
vector<int> d(v+1,INF);
d[startNode] = 0;
cost.push(make_pair(0, startNode));
while (!cost.empty()) {
int nodeNum = cost.top().second;
int weight = -cost.top().first;
cost.pop();
for (int i = 0 ; i<adj[nodeNum].size(); i++) {
if (d[adj[nodeNum][i].first] > adj[nodeNum][i].second + weight) {
d[adj[nodeNum][i].first] = adj[nodeNum][i].second + weight;
cost.push(make_pair(-d[adj[nodeNum][i].first], adj[nodeNum][i].first));
}
}
}
for (int i = 1; i<=v; i++) {
if (d[i]== INF) {
printf("INF\n");
continue;
}
printf("%d\n",d[i]);
}
}
- 만약에 이렇게 2차원 배열로 간선 관계를 저장하면 메모리와 탐색시간이 크다. 따라서 연결 관계만 저장해서 메모리를 아낄 수 있다.
- cost에서 비용이 가장 적은, 아직 방문하지 않은 노드를 선형으로 검색하면 O(n)이 든다. 결과적으로 이렇게 구현한 다익스트라의 복잡도는 O(n^2)이다.
- 우선순위 큐를 활용하면 아직 방문하지 않은 최소 비용의 노드를 찾는데 O(logn)이 되고 결과적으로 O(nlogn)의 다익스트라를 구현할 수 있다.
- cost.push(make_pair(-d[adj[nodeNum][i].first], adj[nodeNum][i].first)); 로 단순히 구현될 수 있는 이유는 다음과 같다. 이미priority queue에 있는 nodeNum의 cost를 갱신하는 것은 어렵다. 아예 그냥 새롭게 노드로 우선순위 큐에 추가해줘도 문제가 되지 않는 이유는 우선순위에 따라 맨 위로 올라올 것이기 때문이다. 제일 마지막에 갱신이 안된(이미 방문한) 노드가 나오더라도 어차피 이는 비용이 큰 경우이므로 d[]의 최단 거리 비용에 영향을 주지 않는다.
- 예를 들면 2번을 경유하게 되어 3, 4, 5 번의 최소비용이 갱신되면 d[]를 바꾸는 것은 물론 priority queue에 들어가 있는 3, 4, 5의 최소비용을 갱신해야 한다. 이게 어려우니까 그냥 새롭게 <3, 최소비용>, <4, 최소비용>, <5, 최소비용>을 우선순위 큐에 넣어버린다. 어차피 최소비용 순서로 튀어나올 거니까 <3, 최소비용>이 기존에 있던 <3, 옛날비용> 보다 먼저 나온다. <3, 최소비용>이 처리 되고나서 남아있는 <3, 옛날비용>은 결과에 영향을 미치지 않는다.
- priority queue 에 거리가 짧은게 우선순위가 높도록 하기위해 -를 붙였고 직접 사용할때는 +로 바꾼다.
'ComputerScience > Algorithm & Data Structure' 카테고리의 다른 글
| Algorithm&DataStructure - Backtracking (0) | 2022.03.17 |
|---|---|
| Algorithm&DataStructure - Map, Set (0) | 2022.02.19 |
| Algorithm&DataStructure - Queue (0) | 2021.08.31 |
| Algorithm&DataStructure - Dynamic Programming (0) | 2021.08.30 |
| Algorithm&DataStructure - BFS (0) | 2021.08.02 |



