1. Linear Discriminant Analysis(LDA, 선형 분리)
- 다차원 공간에 있는 데이터를 1차원 공간으로 Projection 시켜서 분류를 수행하는 것을 말한다.
- 데이터의 class를 가장 잘 분리할 수 있는 공간으로 차원축소하는 것이 목표이다.
- projection을 활용하는데 class를 구분하는 특징을 잘 살려서 축소한다는 점에서 PCA, SVM과 차이가 있다.

- 2차원 공간에 표시된 n개의 데이터에 대해 C1,C2 클래스로 가장 잘 분리되는 1차원 공간을 찾았다.
- 만약 ㅡ 선으로 축소하면 black, blue dot들이 섞여버려서 구분이 어려울 것이다.

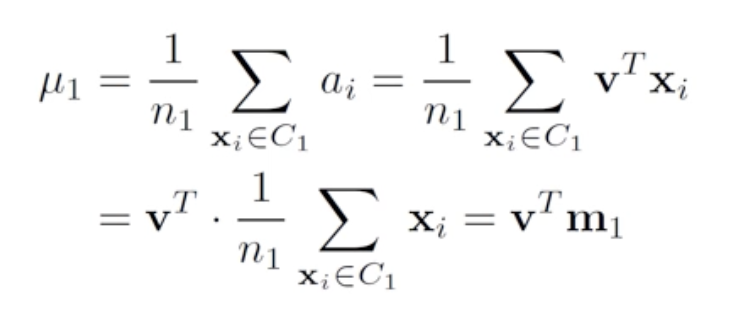

- 어떤 1차원 공간으로 데이터들을 옮겨왔을때 C1(black 점들의 평균)의 평균과 C2(blue 점들의 평균)의 평균이 가장 멀도록 해보자
- projection 결과들의 평균은 원래 공간에서 평균지점을 projection한것과 같다. (m1, m2 를 projection 한 것이 u1, u2)
- |u1-u2|, 거리만 고려하면 ㅡ직선이 더 좋아보일 수 있다.
- 하지만 ㅡ 로 사영시켜버리면 u'1, u'2 사이에 blue, black 점들이 섞이는 공간이 생겨버린다.
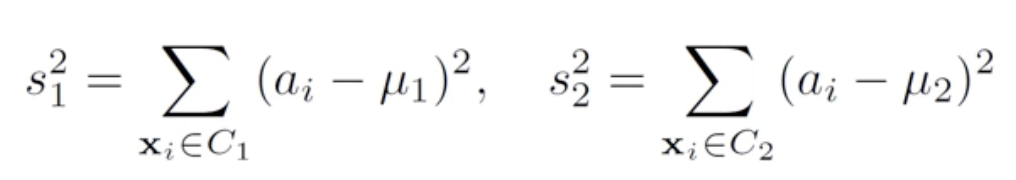
- 즉 오직 평균 거리만이 유일한 척도는 아니라는 것이다. 따라서 projection 공간에서 variance를 최소화 하도록 두번째 척도를 도입한다.
2. 풀기

- 정리하면 projection 했을때 class간의 평균이 가장 멀고, variance가 가장 작도록 하는 직선이 LDA라고 할 수 있다.

- 결국 이 식의 최대값을 찾는 문제로 변환이 되고 v에 대한 식으로 전부 정리하여 미분하면 위 식을 최대로 만드는 v를 찾을 수 있다.
- v는 projection matrix이다.

- 두 class 평균의 제곱 차

- class j의 분산을 구하는 식이다.
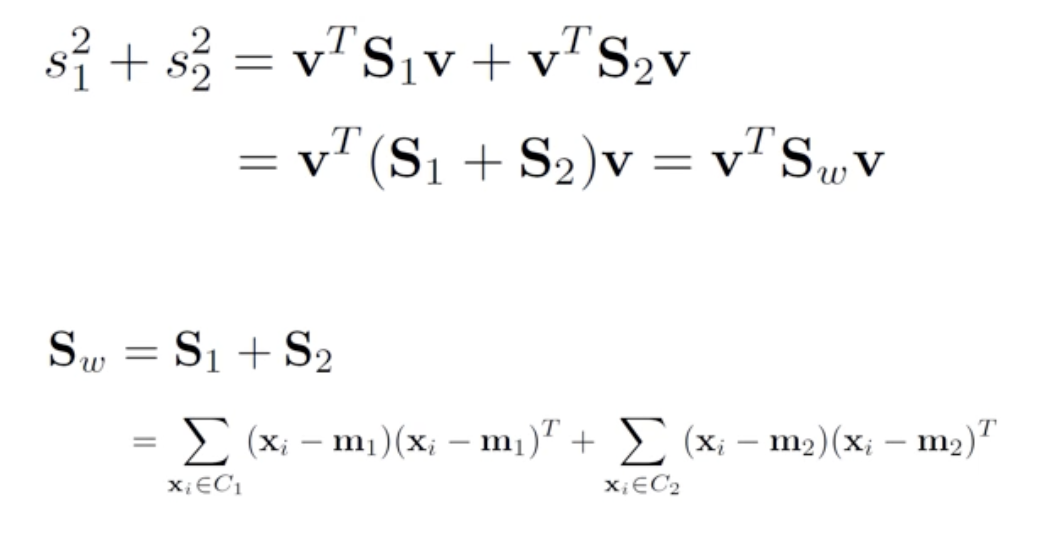
- 만약 class 1,2 가 있다면 각 분산의 합이 total within class scatter 정도가 된다.
3. Solution

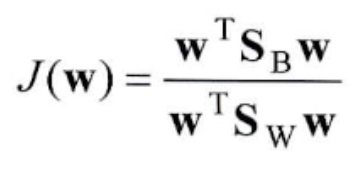
- 이제 v에 대한 식으로 변환도 끝났다. J(w)에 대한 함수로 다시 정의하고, 미분했을때 0이 되도록하는 w를 찾아보자

- 몫의 미분을 했을때 분자만 가져와서 0이 되는 w를 찾는다.
- wTSwW/wTSbw는 1x1 스칼라 값이므로 그냥 a2로 두자. (x가 d차원 공간에 있다고 하면 x는 1xd, project matrix w는 1xd, Sb, Sw는 dxd이므로 곱해보면 스칼라가 된다.)
4. Example

- class 1, class 2로 구분되는 총 6개의 데이터가 있다. LDA를 찾아보자.

- 가장먼저 mean을 구한다

- covariance matrix를 구한다.

- 역행렬과 평균의 차를 곱하면 LDA vector가 나온다.

- LDA로 모든 데이터를 옮기면 위와 같다.
'ComputerScience > Pattern Recognition' 카테고리의 다른 글
| 패턴인식 - 12. Principle Component Analysis (PCA) (0) | 2022.06.02 |
|---|---|
| 패턴인식 - 10. Projection, 차원축소 (0) | 2022.05.26 |
| 패턴인식 - 9. Ensemble - Boosting (0) | 2022.05.20 |
| 패턴인식 - 8. Ensemble - Bagging (0) | 2022.05.13 |
| 패턴인식 - 7. Decision tree (2) (0) | 2022.05.03 |



