1. Projection
- 데이터는 많은 feature들로 구성되어 있다. feature들로 구성된 특징 공간의 차원을 축소하는 방법을 알아본다.

- 3차원 벡터 공간 V를 2차원 linear한 subspace(부분공간, W)로 축소하는 모습이다.
- 3차원 공간의 부분집합 W에서는 덧셈 연산, 스칼라곱 연산을 만족해야 한다. (갇혀 있어야 함)

- projection을 통한 차원 축소 모습이다. (첫번째 그림 e = b - p)
- 3차원 공간의 b벡터를 subspace A로 축소하는 그림이다. 그 변환 매트릭스 P가 정의될 수 있다.
- 이렇게 data를 low dimension space로 mapping하는 것을 dimensionality reduction이라고 한다.
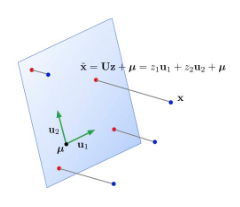
- 그럼 어떻게 적절한 subspace를 찾을 수 있을까?
- 데이터의 평균 u를 설정한다.

- subspace와 모든 data들의 거리(reconstruction error)가 최소가 되는 지점을 찾을 수 있다.
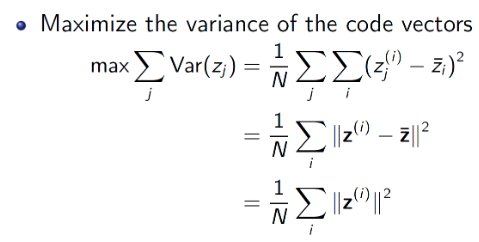
- 혹은 데이터들이 subspace로 사영됐을 때, 퍼져있는 정도를 최대로 하고 싶을 수도 있다. (maximize variance)
- 평균 지점 u로부터 사영된 x~(i)의 거리를 최대로 하는 subspace를 찾는 것이다.
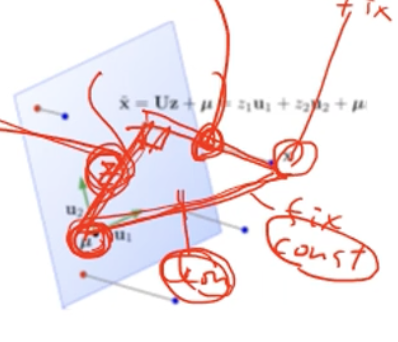
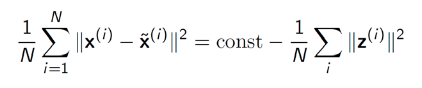

- 데이터와 u의 거리가 상수이기 때문에 피타고라스 정리에 의해 (x(i)와 x~(i)의 차, projection된 결과와 data의 차이)를 최소화 하는 것은 (u와 x~(i)의 거리)를 최대로 하는 것과 사실 동일한 방법이다.
- 이렇게 결정한 subspace의 u1,u2 벡터를 PCA(principle component)라고 한다.
2. 정리
- 데이터의 차원을 낮추는 이유는 뭘까?
- 데이터의 차원을 낮추면 작업 수준(복잡도, 연산량)을 낮출 수 있다.
- 실제로 우리는 2차원 공간내에서 대부분의 문제에 대해 솔루션을 찾을 수 있다. 하지만 3차원으로 올라가기만 해도 못푸는 문제가 생각보다 많다.
- 따라서 정보의 손실을 최소화 하면서 내가 문제를 해결할 수 있는 정도까지 차원을 축소하는것이 목표이다.
'ComputerScience > Pattern Recognition' 카테고리의 다른 글
| 패턴인식 - 12. Principle Component Analysis (PCA) (0) | 2022.06.02 |
|---|---|
| 패턴인식 - 11. Linear Discriminant Analysis(LDA) (0) | 2022.06.02 |
| 패턴인식 - 9. Ensemble - Boosting (0) | 2022.05.20 |
| 패턴인식 - 8. Ensemble - Bagging (0) | 2022.05.13 |
| 패턴인식 - 7. Decision tree (2) (0) | 2022.05.03 |



