1. BCNF
- BCNF의 정의를 살펴보자.
- BCNF인가를 따지려면 일단 모든 함수 종속관계를 알고 있어야 한다.
- 그 종속관계중에서 trivial 한것은 당연히 아래 첫번째 조건을 만족하고 non trivial 한 관계는 아래 제시된 조건을 만족해야 한다. 그럼 BCNF가 된다.

- non trivial 한 종속관계에서 결정자가 superkey이면 된다.

- 이 예시를 보면 dept_name -> building, budget 이라는 non trivial 함수 종속관계가 성립은 하지만 a부분인 dept_name은 슈퍼키가 아니다. 따라서 이 테이블은 BCNF의 조건에 위배된다.

- 실제로 테이블을 보면 동일한 dept_name이 여러번 나오기 때문에 고유식별성이 없다. 따라서 함수종속이 성립하더라도 BCNF가 될 수 없다.
*즉 non trivial 한 함수 종속관계가 있을때 결정자 a는 고유식별성이 있어야 BCNF가 될 수 있다.
2. BCNF로 decomposition하기

- BCNF가 아닌(non trivial 한 종속관계에서 결정자가 고유식별성이 없음) R을 분해해 보자.
- 계속 bad design예시로 들었던 in_dep을 분해하는 방법이 위에 나와 있다.
- BCNF 형태가 될때까지 쪼개기를 위 공식으로 반복한다.

- 결과적으로 이렇게 쪼개진다.
- BCNF로 쪼개는 다른 예시를 살펴보자.

- class에 존재하는 non-trivial한 모든 함수 종속관계를 먼저 찾는다.
- 그 관계들중 결정자가 슈퍼키인지 확인한다. 이 법칙에 위배되는 부분을 아까 배운 공식에 따라 decomposition한다.
- 이제 다시 course와 class-1이 BCNF인지 확인한다.
3. BCNF 정규화 예제 1

- 이런 현실세계의 제약이 있는 은행 대출 관리 DB를 예로 들겠다.

- 여기에 존재하는 non-trivial한 함수 종속관계를 나열해보자.
- 고객 테이블에서 이름이 연락처를 결정하지 않지만 고객ID는 한명의 이름과 연락처를 결정할 수 있다.

- erd모델로 부터 도출한 테이블 스키마가 BCNF 형태를 이루는지 확인해보자.

- 5개의 테이블 모두가 BCNF인지 확인한다. a(알파)가 고유식별성이 있는지 확인한다.
- 대출 고객 테이블을 보면 고객ID가 대출 번호를 결정하지 않는다 (같은 고객이 여러번 대출을 받을 수 있음) 이 테이블에서는 함수 종속관계가 없다. 여기에는 trivial FD만 존재한다.
- 모두 BCNF 형태이기 때문에 good 스키마라고 볼 수 있다.
4. BCNF 정규화 예제 2
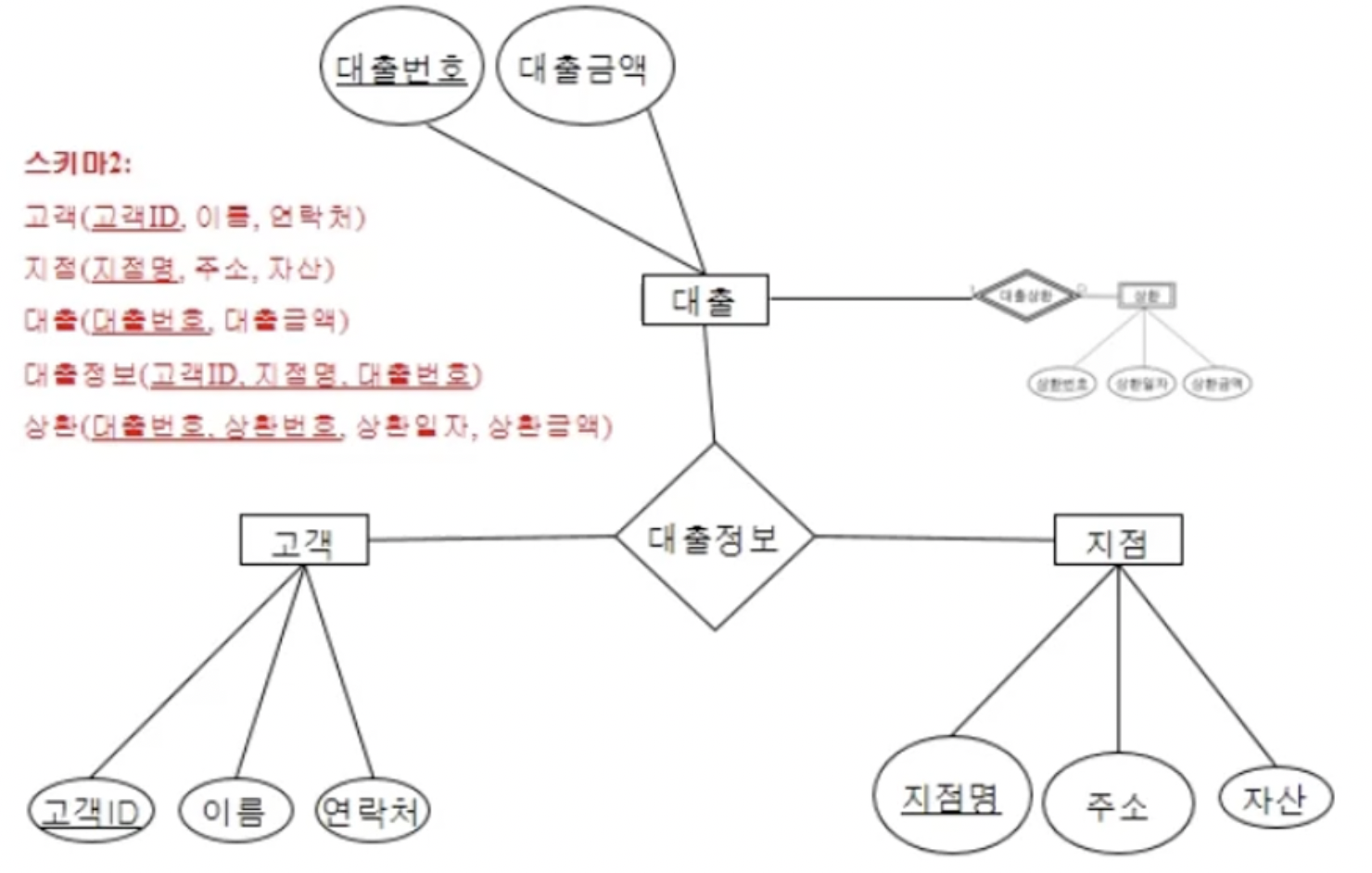
- 이번엔 1번 예제와 동일한 현실 제약을 가지지만 다른형태로 도출된 스키마를 정규화 해보자.

- 마찬가지로 테이블별로 만족하는 함수 종속관계를 파악하고 BCNF인지 확인한다.
- 대출정보를 제외하고는 모두 BCNF를 만족한다.
- 대출정보 테이블에서 대출번호는 특정 지점을 결정하는데 대출번호 단독은 superkey가 아니기 때문에 BCNF가 아니다.
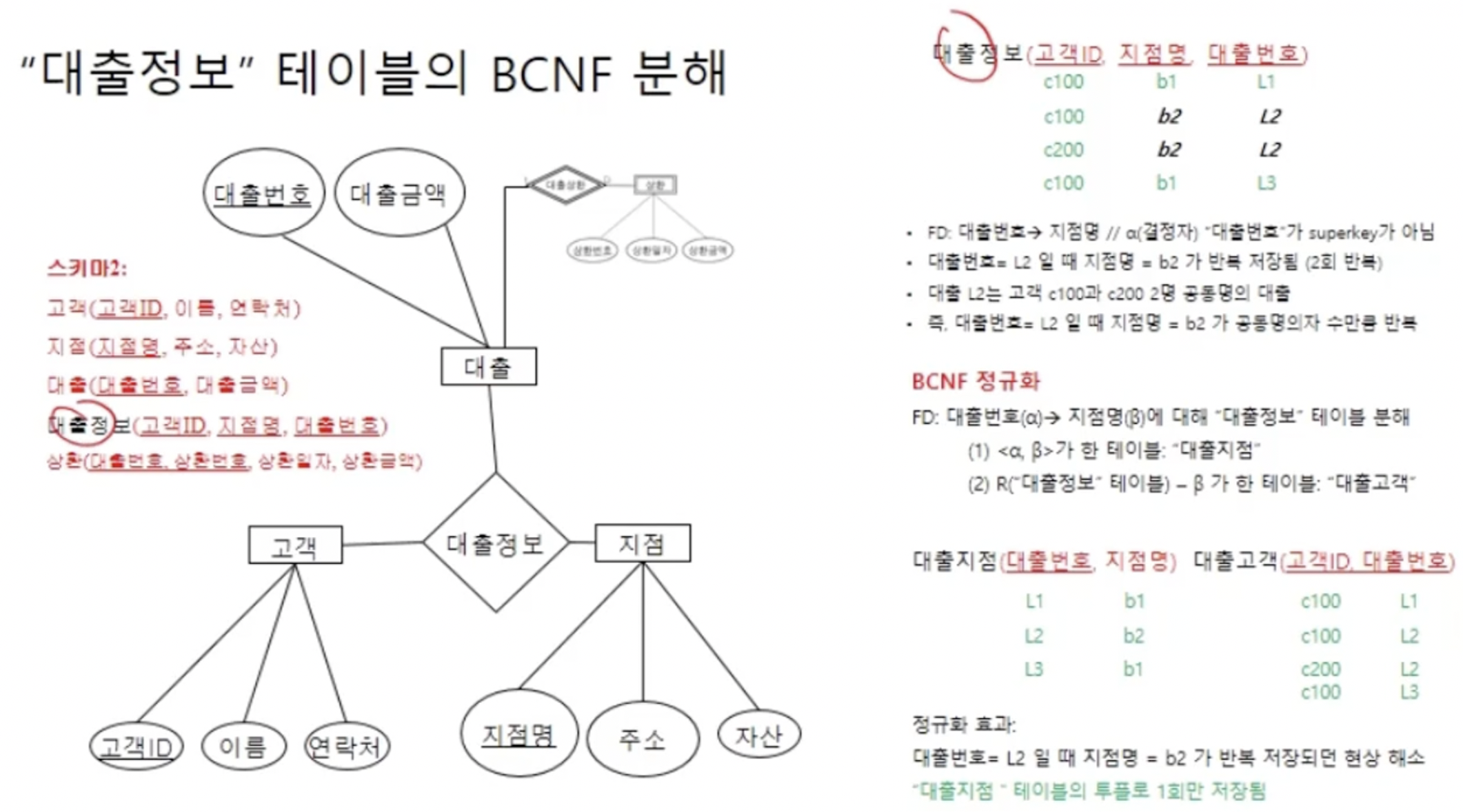
- 실제로 대출정보 테이블에서 먼저 어떤 문제가 발생할 수 있는지 살펴보자.
- C100, C200이 공동명의로 b2지점에서 L2번호 대출을 받은 경우가 있을 수 있다.
- 이런 종류의 레코드는 공동명의자 수만큼 데이터의 중복을 유발한다.
- 따라서 BCNF공식에 따라 decomposition을 수행한다.

- 쪼갠 결과에 대해서 다시 모든 테이블이 BCNF형태인지 확인한다.

- 이렇게 새롭게 도출된 스키마를 그냥 써도 되지만 정제과정을 거쳐서 더 좋은 스키마를 도출할 수 있다.
- 여기서는 대출 테이블과 대출지점 테이블의 통합이 이루어져 더 좋은 스키마가 도출되었다.
'ComputerScience > Database' 카테고리의 다른 글
| DB - 19. Intermediate SQL - Join (0) | 2021.11.30 |
|---|---|
| DB - 18. Normalization 2 (0) | 2021.11.30 |
| DB - 16. Normalization (0) | 2021.11.23 |
| DB - 15. University Enterprise ER -> RDB (0) | 2021.11.23 |
| DB - 14. E-R Model, RDB로 변환하기 2 (0) | 2021.11.15 |



