1. Normalization
- db를 구축하기 위해 거치는 단계를 정리하면 요건 분석 -> ERD -> Table 스키마 였다.
- 하지만 요건분석 -> ERD는 특정한 규칙에의해 이루어진다기 보다는 설계자의 의도에 의해 정해지기 때문에 오류가 생길 가능성이 항상 있다.
- 그래서 변환규칙으로 만들어진 table 스키마가 항상 good design이라고 장담할 수 없기 때문에 이를 정제하는 과정이 필요하다.
2. Good design? Bad design?
- good design, bad design이 무엇인지 살펴보자.
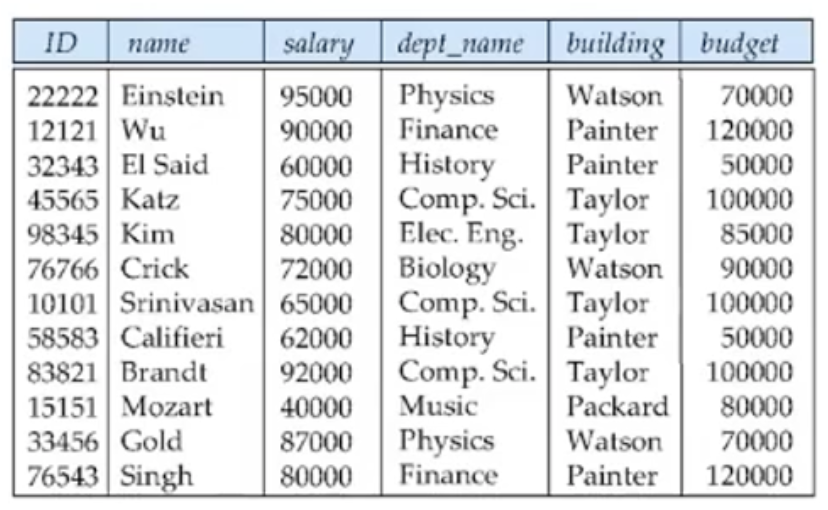
- 이 테이블은 department와 instructor가 함께 하나의 테이블로 구성되어있다.

- 이 디자인이 bad design인 이유로 들 수 있는 것은 학과 데이터의 중복이다.
- 보면 Comp. Sci가 여러번 반복되어 record의 속성으로 기입된다. (교수 수만큼 반복됨)
- 두번째 이유는 null값이 들어갈 가능성이 있다. 예를들어 새로운 학과가 생겼는데 아직 교수가 배정되지 않은 상태라면 null이 들어간다.
- 심지어 아래 레코드를 보면 고유식별자 까지 null이 들어가버린다.

- 세번째 이유는 만약 저 테이블에서 Mozart교수가 퇴임하여 record를 지우려한다면 덩달아 Music department도 사라져 버릴 수 있다.
- 하지만 마냥 중복을 제거하겠다며 테이블을 분리하는 것이 좋은 것은 아니다.

- 이런경우는 오히려 합하는 것이 나은 경우이다.
3. Decomposition
- 위에 예시에서 살펴봤듯 테이블을 분해하는 작업이다.
- 하지만 절대적으로 쪼개는 것이 정답은 아닐 수 있다. (아래 예시)


- 나중에 join 연산을 할때 동명이인끼리 묶여버려서 실세계에 없는 조합이 생길 수도 있다.
- 이렇게 잘못된 분해로 정보의 손실이 생기는 것을 Lossy Decomposition이라고 한다.
- 따라서 분해를 할때는 손실이 발생하지 않는 lossless decomposition을 수행해야 한다.
- lossless decomposition의 조건을 수식으로 표현하면 아래와 같다.


- R1과 R2가 R을 decomposition 한 것이라면 두 relation의 자연조인이 r로 복귀 되어야 한다.
- lossy decomposition은 아래의 경우이다.

4. 중간정리
- 정리하면 R이 bad form이라면 decomposition을 통해 R을 {R1, R2,...,Rn} 모두가 good form이 되도록(lossless decomposition) 분해하는 것이 normalization이다.
- 이렇게 분해된 relation 들은 BCNF가 된다.
- normalization은 두가지 이론에 근거해서 이루어진다. 이어서 하나씩 알아보자.
5. Functional Dependency
- 현실 세계에서는 다양한 제약이 존재한다. 예를들면 교수이름은 하나이며 특정 학과는 특정 건물을 사용한다는 등 테이블에 column들 간에 종속관계가 존재한다.
- 아래 예시를 보면 department마다 budget과 사용하는 건물이 정해져있다. dept_name을 결정자, building, budget을 종속자라고 한다.

- y = f(x)처럼 결정자가 들어가면 유일한 종속자가 나오는 관계를 맺고 있기 때문에 함수 종속성이라고 한다.

- a, b 모두 R의 속성중 하나이다.
- a -> b : a가 b를 결정하는 관계이다.
- 이 종속 관계는 t1 튜플이나 t2튜플이나 모두 동일하게 적용된다.
- a가 들어가면 b는 유일하게 결정되어야 한다. 위의 예시를 보면 B -> A는 유니크하게 결정되지만 반대의 경우는 1이 들어왔을때 4, 5가 될 수 있기 때문에 종속관계 성립이 불가능하다.

- 만약 A->B 이고 B->C라면 주어지지 않더라도 A->C임을 추론할 수 있다.
- 이렇게 제시된 모든 함수 종속관계들과 그 관계들의 추론으로 도출되는 종속관계를 모두 모은 집합을 closure라고 한다.

- 당연한 얘기지만 그 테이블의 고유식별자는 모든 다른 column들과 종속관계를 갖는다.

- 고유식별자 ID를 갖는 튜플은 유일하기 때문이다.

- Department table에서 종속관계를 식으로 표현하면 아래와 같다.
- 한가지 특이해 보이는 건 dept_name -> dept_name이다. 이런 식은 항상 자동으로 성립한다. Biology -> Biology처럼 반드시 성립되는 관계이다. 이런 관계를 trivial functional dependencies라고 한다.


- 이렇게 하나로 모아서 쓸 수도 있다. 근데 잘 살펴보니까 dept_name, building, budget은 사실상 테이블의 전체 속성이다.
- 따라서 dept_name -> Department 처럼 표현도 가능하다.

- 따라서 K가 superkey라면 K -> R이 성립한다.
- 여기서 배운 내용을 가지고 lossless decomposition의 조건을 정의해보자.

- R1 과 R2로 분해할때는 반드시 겹치는 column이 존재한다. 따라서 R1과 R2의 교집합은 R1을 결정하거나 R2를 결정한다.
- 교집합의 column이 R1또는 R2를 결정하려면 그 column은 R1또는 R2의 고유식별자여야 한다.
- 두 식중 하나를 만족하면 lossless decomposition이라고 할 수 있다.
- 아래는 R = {A, B, C}를 R1 = (A, B), R2 = (B, C)로 쪼갰을 때 lossless decomposition이 성립하는지 증명하는 예시이다.

'ComputerScience > Database' 카테고리의 다른 글
| DB - 18. Normalization 2 (0) | 2021.11.30 |
|---|---|
| DB - 17. Boyce Codd Normal Form (0) | 2021.11.24 |
| DB - 15. University Enterprise ER -> RDB (0) | 2021.11.23 |
| DB - 14. E-R Model, RDB로 변환하기 2 (0) | 2021.11.15 |
| DB - 13. E-R Model 4 (0) | 2021.11.15 |



