1. Schema Diagram 분석
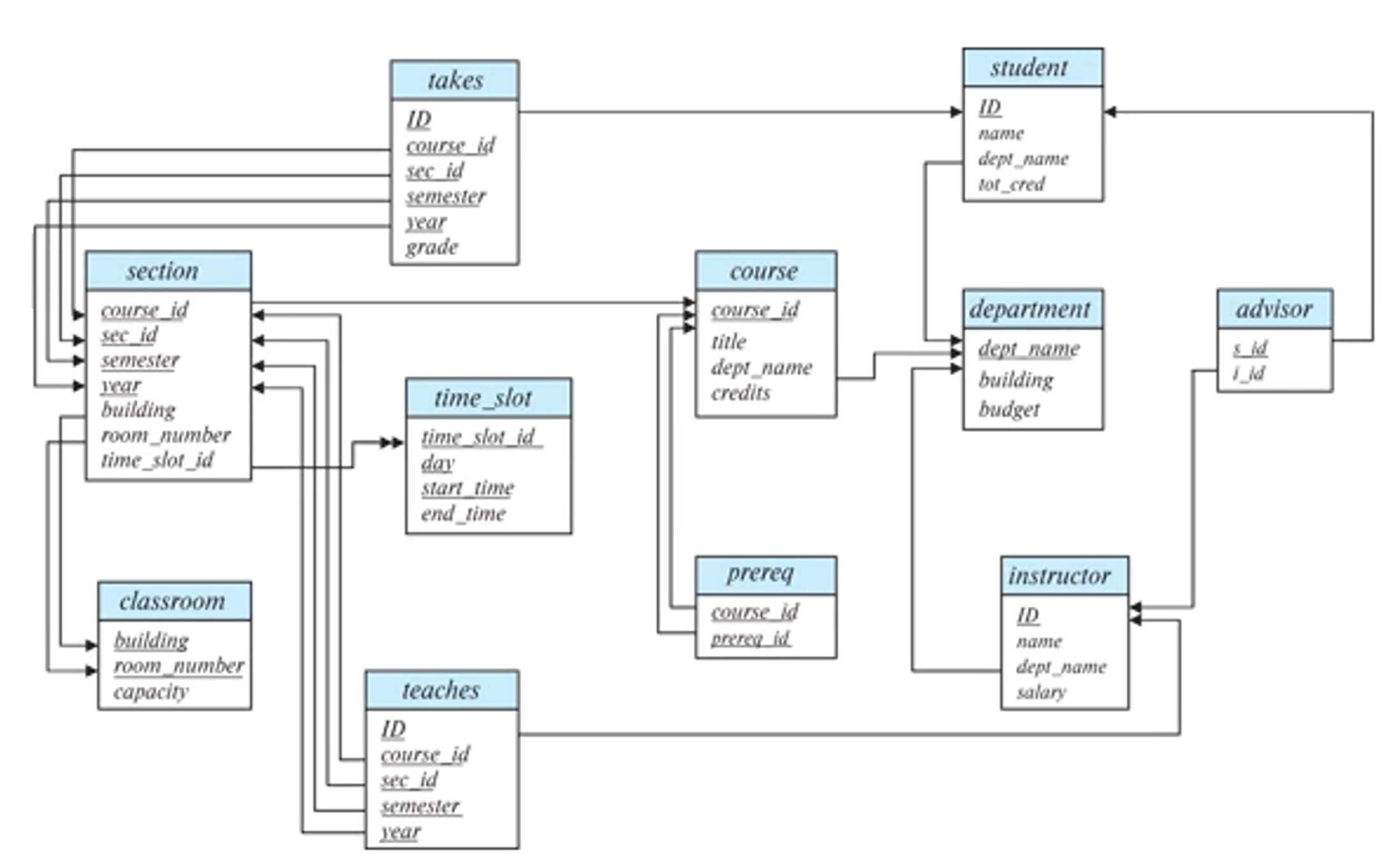
- 사각형 하나가 relation에 해당한다.
- 각 relation들의 reference관계를 화살표로 나타내고 있다.
- relation에서 밑줄이 그어진 column이 Primary key이다.
- takes relation의 경우 (ID, course_id, sec_id, semester, year)가 primary key이다. 이 경우는 composite key이기도 하다.
- 하나의 relation에서 다른 relation으로 foreign key를 통해 연결된다. 화살표가 출발하는 쪽이 foreign key, 화살표가 도착하는 곳이 primary key여야 한다.
- 복수개의 column으로 이루어진 foreign key도 존재할 수 있다. 복수개의 column으로 구성해야 도착 relation에서 고유식별성을 지닐 수 있는 경우에 해당한다. 즉 여러개의 column들이 합성된 하나의 foreign키가 되는 것이다.
- section에서 time_slot으로 이어지는 화살표를 보면 화살표 머리가 두개이다. 이 화살표는 외래키가 성립하지는 않지만 참조관계는 있음을 의미한다.
2. Relational Algebra
- 아래 기본적인 6개의 연산자를 나열하였다.
- relational DB에서 필요한 데이터를 가져오기 위한 수학적 표현식을 살펴보자.

Select
- 아래첨자의 조건을 만족하는 relation을 () table에서 가져온다.
- reuslt는 반드시 relation으로 반환된다.

- 같다, 다르다, 크다, 작다, and, or, not 등의 여러 조건을 활용할 수 있다.
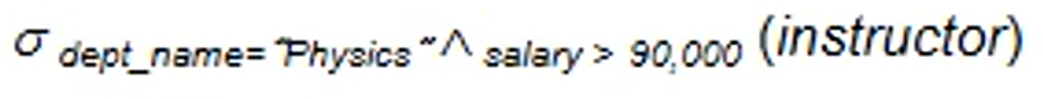

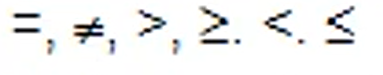
Project
- () relation에서 아래첨자에 해당하는 property만으로 구성된 relation을 반환한다.
- 만약 새로운 relation을 구성할때 중복되는 row가 생기면 중복을 제거한 채로 relation을 만들어 반환한다.

- 아래처럼 여러 operation을 함께 사용할 수 있다.

Cartesian product
- 두 개의 relation에 대해 x를 수행한다. 그럼 두개의 relation에서 각각 tuple들을 꺼내서 짝을 만든다.

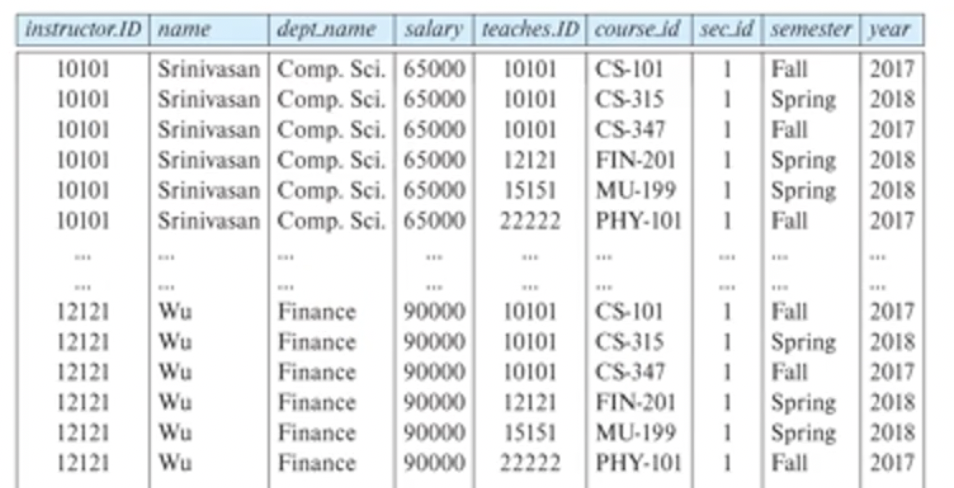
- instructor, teaches 두 relation에 대해서 곱을 수행하면 위와 같다. 만약 instructor(10개 tuple) teaches(100개 tuple)이라면 총 연산 결과는 1000개의 tuple을 갖는다.
- wu 교수는 실제로 cs-101과목을 가르치지 않는다. 즉 이렇게 의미없는 짝들이 생길 수 있으니 조건을 잘 활용해서 걸러내야 한다.
Join
- cartesian product 연산을 기본으로 하되 조건을 추가해서 의미있는 table을 만들어낸다.

- 위의 예시에서 교수 정보와 해당 교수가 가리키는 과목에 대한 정보를 합쳐서 새로운 table을 만드는 방법이다.

- 정리하면 r, s relation의 product결과에서 theta의 조건을 만족하는 tuple들을 반환한다.
Natural Join


- theta가 빠져있다면 natural join이다.
- 두 테이블에서 이름이 같은 column간의 equal조건으로 join을 수행한다.
- r과 s를 join 하되 중복되는 이름의 column을 제거한다. 즉 결과물에서는 A column이 하나만 존재한다. 그냥 join과의 차이점이다.
- 만약 r(A,B,C,D), s(A,B,E,F)라면 natural join시 A=A ^ B=B 가 조건이 된다. 결과는 (A,B,C,D,E,F)가 된다.
Union
- 두개의 relation을 합치는 연산이다.
- union 이 가능하려면 두가지 조건이 필요하다. 두 relation의 attribute 수와 해당 속성의 domain이 동일해야 한다.
- union연산은 자동으로 중복되는 tuple을 제거해 준다.


- section에서 fall, 2017 수업만 뽑고, 다시 section에서 spring, 2018 수업을 뽑고 두 relation을 union하는 예시이다.
Intersection
- 두 relation에서 공통된 tuple만 반환한다.
- 두 relation은 동일한 attribute 수와 동일 범위 attribute domain을 가져야 한다.

Difference
- 두 relation에서 차집합 연산을 수행한다.
- 두 relation은 동일한 attribute 수와 동일 범위 attribute domain을 가져야 한다.

Assignment
- 할당 연산자이다. 연산의 결과를 어떤 변수에 저장하는 연산을 수행한다.

- 연산의 결과를 Physics, Music 라는 변수에 담아서 다음 연산에 활용한다.
Rename
- 연산의 결과로 얻어지는 새로운 relation에 대해 새로운 이름을 붙이는 연산이다.
- product 연산을 하기 전, 각 relation의 중복되는 column들의 이름을 바꾸는 경우에 종종 사용한다.

- E라는 식이 반환하는 relation에 x라는 이름을 붙인다.

- E라는 식이 반환하는 relation에 x라는 이름을 붙이고 각 column에 A1, A2, .. An이라는 이름
을 붙인다.
* 동일한 결과에 대해서 다양한 식의 표현이 있을 수 있다


Division
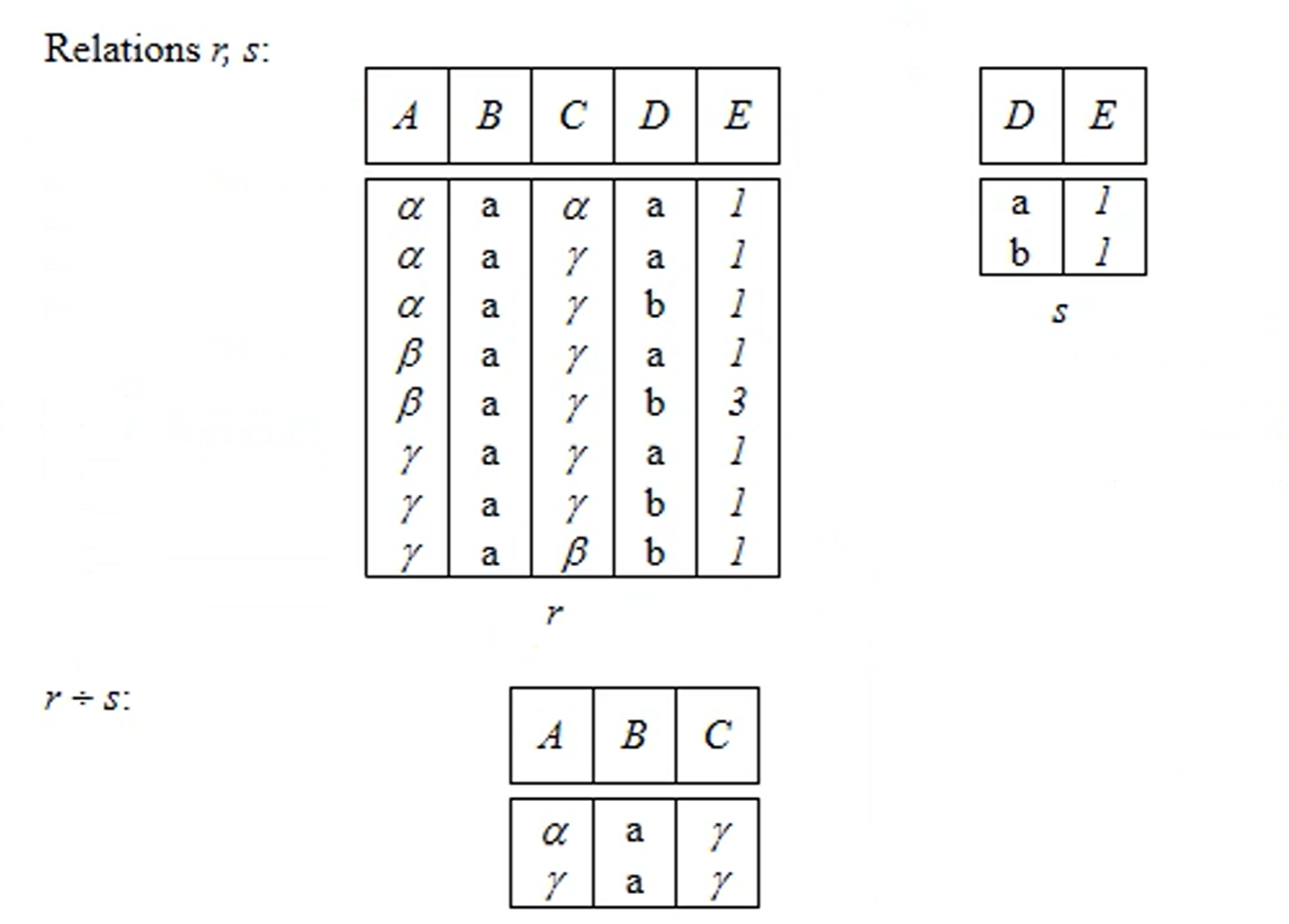
- s를 모두 품고 있는 새로운 relation (A,B,C)를 반환한다.
- 나누기 연산은 따로 없다. 기존의 연산자를 통해 구현해야 한다.


'ComputerScience > Database' 카테고리의 다른 글
| DB - 7. More SQL statements(2) (0) | 2021.10.06 |
|---|---|
| DB - 6. More SQL statements(1) (0) | 2021.09.29 |
| DB - 4. Keys (at relational DB) (0) | 2021.09.15 |
| DB - 3. Relational Database (0) | 2021.09.08 |
| DB - 2. Basic SQL statements (0) | 2021.09.08 |



