1. Terms
Syntax : form, structure, grammar of expression(statement)
Semantic : meaning of the expression(statement)
sentence : string of characters
language : set of sentences
lexeme : lowest level syntatic unit (ex. int, age, =)
token : category of lexeme (e.g. identifier, type)
Recognizer : parser, parse sentence into a tree, check input wheter it belongs to the language
Generator : generate IR
syntax는 문장의 구성 방식을 정의한다. 예를들어 변수 =(대입) 값 같이 문장 구성의 순서등을 정의한다.
semantic은 문장이 의미론적으로 올바른지를 규정한다. 예를들어 int age = 11.3은 정수형 대입이 아니므로 틀렸다.
syntax와 semantic은 프로그래밍 언어의 문법을 규정한다.
lexeme은 syntax 판단을 위해 쪼갠 가장 작은 구성 요소이다. (int, age, =)
token은 lexeme의 카테고리를 말한다. (type, identifier)
2. Syntax
Programming Language syntax helps programmer learning what is allowed and what is not.
Using syntax, compiler can understand programs and enforce the syntax for the program to be valid.
Input, sentence is a series of bytes, characters. (ex. int age = 35;)
First assemble the string of characters into something that a program can understand
so the output should be a series of tokens
3. 1 Context free grammar
syntax를 표현하기 위해 사용하는 방법이다.
terminal, non-terminal, rule, start symbol 네가지로 자연어의 문법을 구성할 수 있다.
BNF는 CFG 개념을 활용한 syntax 표현 방법이다.
G = (S, N, T, P)
S: Starting Symbol
N: Non-terminal
T: Terminal
P: Production Rule
3. Backus-Naur Form (BNF)
tool for describing language's grammar with mathmatical expression
<digit> → 0 | 1 | 2 | … | 9before -> : LHS (left hand side)
after -> : RHS(right hand side)
-> : derive sign, derivation
<digit> can be one of 0~9
<> : non-terminal symbol, can be derived more
0~9 : terminal symbol, can not be derived anymore, leaf node, terminals are lexemes or tokens
<assign> → <var> = <expr><assign> : start symbol, non-terminal
before -> : LHS (left hand side), only non-terminal
after -> : RHS(right hand side), non-terminal or terminal
|, =, → : meta symbol
4. BNF Rules
Let's say we have a BNF rule (grammar)
<number> → <number><digit> ────── ➀
| <digit> ────── ➁
<digit> → 0 | 1 | 2 | … | 9 ────── ➂Then we can derive 123 like this
<number> ⇒ <number><digit> ─ by ➀ <number> -> <number><digit>
⇒ <number><digit><digit> ─ by ➀ <number> -> <number><digit>
⇒ <digit><digit><digit> ─ by ➁ <number> -> <digit>
⇒ 1<digit><digit> ─ by ➂ <digit> -> 1
⇒ 12<digit> ─ by ➂ <digit> -> 2
⇒ 123 ─ by ➂ <digit> -> 3
<number> is the start symbol. and like this we've derived 123


5. Derivation practice (leftmost, rightmost)
Derive A = B * (A + C)
<assign> → <id> = <expr>
<id> → A | B | C | D
<expr> → <id> + <expr>
| <id> * <expr>
| (<expr>)
| <id>Q1. Left most derivation
<assign> → <id> = <expr>
→ A = <expr>
→ A = <id> * <expr>
→ A = B * <expr>
→ A = B * (<expr>)
→ A = B * (<id> + <expr>)
→ A = B * (A + <expr>)
→ A = B * (A + <id>)
→ A = B * (A + C)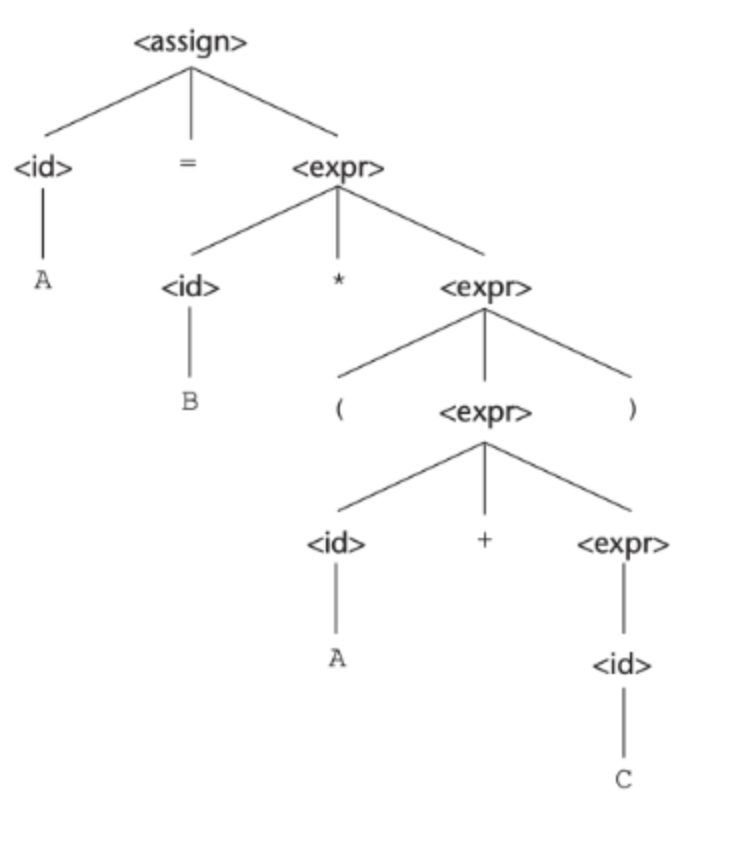
Q2. Right most derivation
<assign> → <id> = <expr>
→ <id> = <id> * <expr>
→ <id> = <id> * (<expr>)
→ <id> = <id> * (<id> + <expr>)
→ <id> = <id> * (<id> + <id>)
→ <id> = <id> * (<id> + C)
→ <id> = <id> * (A + C)
→ <id> = B * (A + C)
→ A = B * (A + C)6. Parse Tree
Representation of derivation
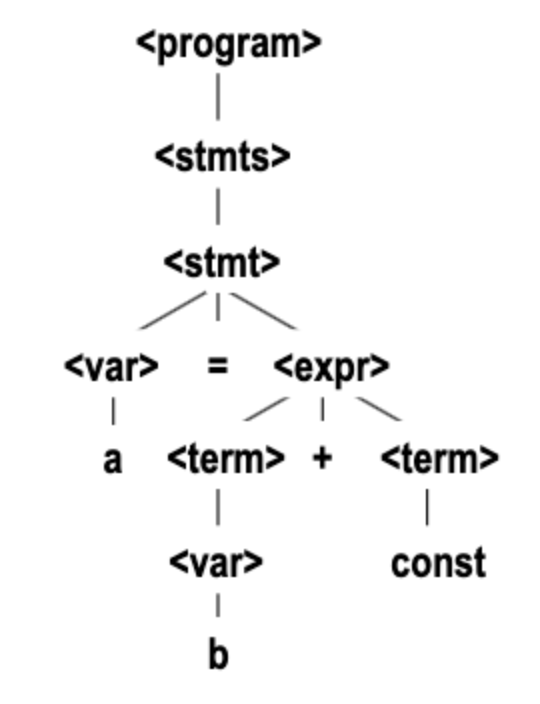
7. Ambiguity in Grammars
Providen grammar, different parse tree produce the same result. We call this ambiguity which belongs to wrong grammar.
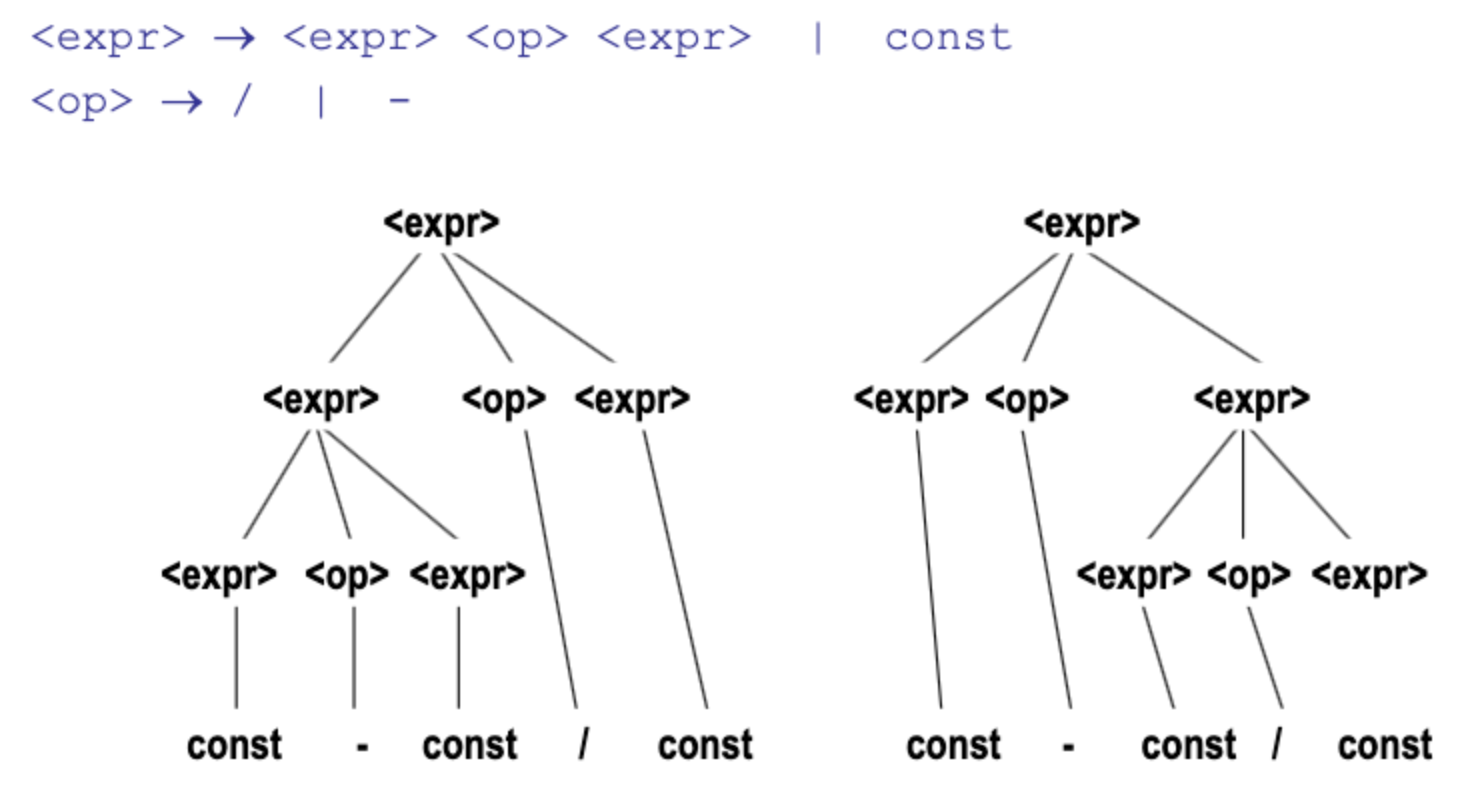
To solve this ambiguity. we have to add disambiguating rule.
So that we can derive the same result no matter which derivation you take.

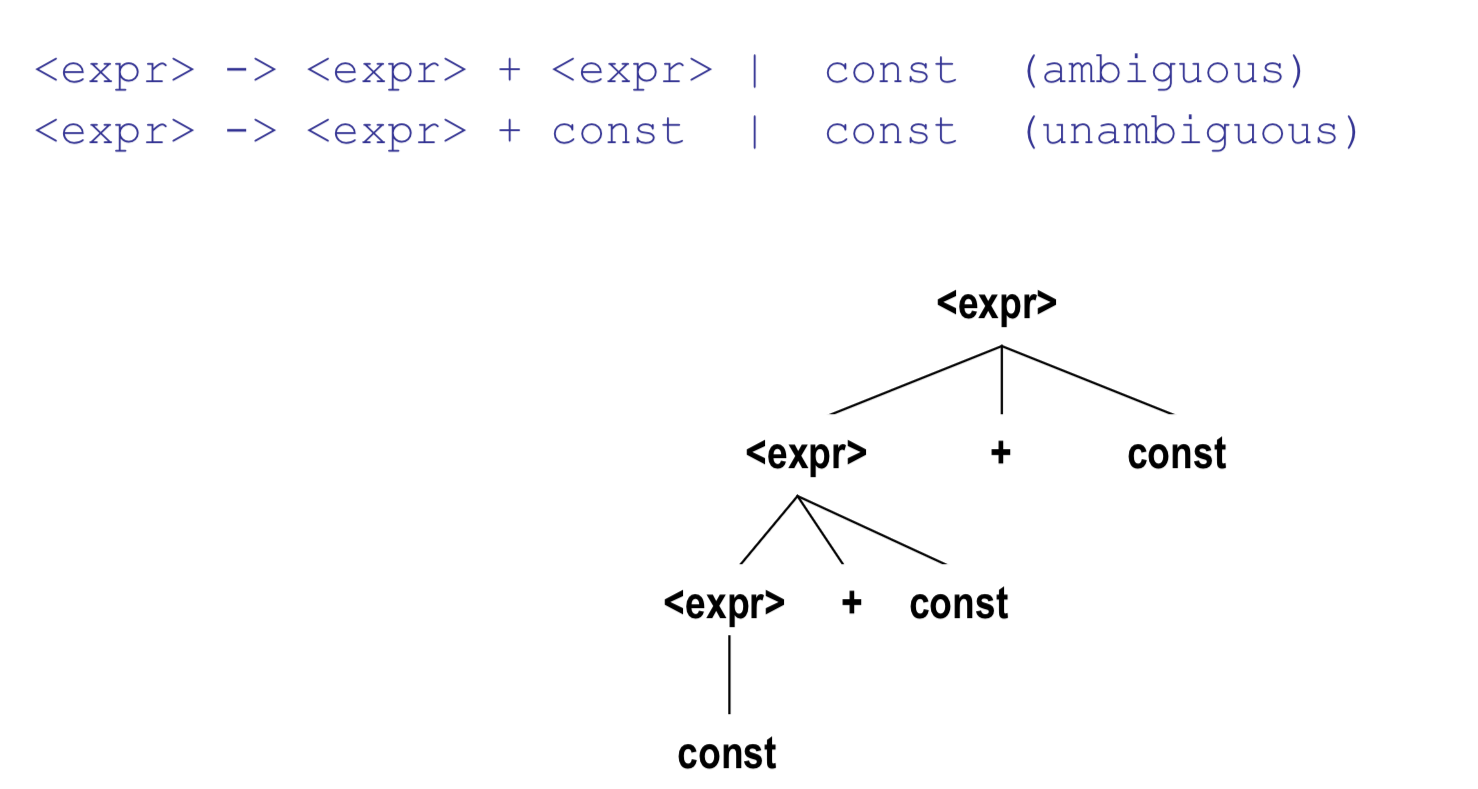
8. Extended BNF (EBNF)
<proc_call> -> ident [(<expr_list>)]
<if_stmt> -> if (<expr>) <stmt> [else <stmt>][] : optional part
<term> -> <term> (+|-) const(+|-) : + or -
<indent> -> letter {letter | digit}{} : repetition
ex) <id> -> letter letter digit letter

'ComputerScience > Principle of programing language' 카테고리의 다른 글
| PL6. Syntax Analysis - top down parsing (0) | 2023.10.06 |
|---|---|
| PL5. Dynamic semantics : Axiomatic (0) | 2023.10.04 |
| PL4. Dynamic semantics : Operational, Denotational (0) | 2023.09.27 |
| PL3. Static semantic (0) | 2023.09.15 |
| PL1. Programming Languages? (0) | 2023.09.14 |



