네트워크는 2개의 주요 기능이 있다고 했다.
- 패킷을 router의 Input에서 올바른 output으로 이동시키는 forwarding(data plane)
- src에서 dst으로 패킷을 전달할 경로를 결정하는 routing(control plane)
1. Per-router control plane

모든 router에서 각각 forwarding table을 만든다. routing algorthim으로 table을 만들고 관리한다.
2. Logically centralized control plane(SDN)
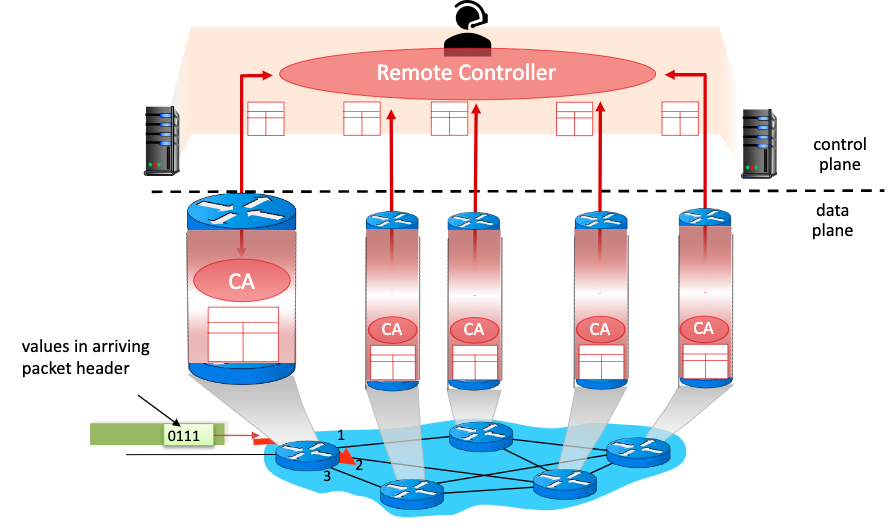
각 router안에 있는 local control agent(CAs)가 (보통 원격으로 따로 존재하는) controller에게 정보를 보내준다.
그럼 controller가 알고리즘으로 각 router의 forwarding tables를 만들어 각각 전송해준다.
3. routing protocol
sending host에서 receiving host까지 패킷의 good path를 찾는 것이 목적이다.
네트워크 어플리케이션의 상황, 목적에 따라 least latency 혹은 highest throughput, least congestion등이 good의 기준이 될 수 있다.

네트워크를 graph로 추상화 하였다. router(vertex), link(edge), cost(weight)

path의 비용은 위처럼 표현할 수 있다.
최소 비용 경로로 패킷을 전달하고 싶다면 예를들어 u에서 z로 가는 최소 비용 경로를 찾는 문제로 생각할 수 있다.
(global) 만약 지금처럼 전체 네트워크 모양(비용, 연결관계)을 알고 있다면 "link state" algorithm으로 문제를 해결할 수 있다. (link state 말고 다른 알고리즘도 있다.)
(decentralized) 하지만 router가 전체 네트워크의 topology를 모르고 직접 물리적으로 연결된 이웃 정보만 알고 있다면 반복적인 계산을 통해 답을 구하는 "distance vector" alogorithm으로 문제를 해결할 수 있다. (link state 말고 다른 알고리즘도 있다.)
네트워크를 구성하는 라우터가 변하지 않는 환경에서는 알고리즘이 아주 가끔 돌면 된다.
하지만 무선환경처럼 라우터가 자주 바뀌는 경우는 알고리즘이 수시로 table정보를 업데이트 해줘야 한다.
4. link state
router가 network topology(complete graph)를 알고 있을 때 path를 찾는다.
Dijkstra's algorithm 은 link state algorithm 중 하나이다.
모든 router가 broadcast로 자신의 위치를 다른 모든 router에게 알림으로써 각각 network topology를 알도록 한다. (centralized algorithm)
다익스트라 알고리즘은 한 시작 노드에서 다른 노드들로 가는, 가중치를 고려한 최단경로 찾기 알고리즘이다.
다익스트라 알고리즘은 greedy algorthm이다.
이렇게 찾은 경로들로 forwarding table을 만든다.

c(x,y) : x에서 y로 가는데 드는 비용 (link)
D(v) : source node에서 v로 가는 path의 비용
p(v) : path에서 v 노드 직전의 노드
N' : 최단 경로 계산을 완료한 목적지 노드의 집합
*N개의 노드로 네트워크가 구성되어 있다면 Loop를 N-1번 반복하면 된다.
*비용이 같은 서로 다른 경로가 있다면 아무거나 선택하면 된다.

각 노드에 대해 predecesor node만 표시한 것을 shortest-path tree라고 한다.

또 다른 예시이다. 최종적으로 shortest-path tree를 구하면 이것이 forwarding table이 된다.
*위에서 예제로 연습한 방식의 복잡도는 O(n^2)이다. 하지만 priority queue(heap으로 구현)를 활용하면 O(nlogn)으로 복잡도를 개선할 수 있다.
oscilliation
link의 cost를 static한 값으로 설정하지 않고 그때그때 트래픽에 따라 달라지도록 했다고 해보자. (link cost는 traffic의 양과 같다고 가정한다.)

C로 들어오는 traffic이 e, D는 1, B는 1이라고 하자.
그럼 초기에 cost가 전부 0일때, shortest-path tree는 맨 좌측 그림과 같다.
두번째는 상황이 바뀌었다. B는 A로 바로가는 것보다 C, D를 거치는게 더 비용이 적다고 판단하고 이는 다른 노드에서도 마찬가지이다. shortest-path tree가 바뀌었다.
세번째도 C의 경우 더 이상 D를 거치지 않고 B를 거치는 경로를 선택한다. 또 shortest-path tree가 바뀌었다.
이런식으로 link cost가 dynamic하게 바뀌는 경우 매번 forwarding table을 다시 구하게 되는 상황을 osciliation이라고 한다.
5. distance vector
router가 전체 네트워크의 topology를 모르고 직접 물리적으로 연결된 이웃 정보만 알고 있을때, path를 찾는 방법이다.

Bellman ford algorithm은 대표적인 distance vector 알고리즘 중 하나이다. dynamic programming algorithm으로 접근한다.
u에서 시작해서 z로 가는 최단경로를 찾는 예시이다. u와 연결된 v,x,w 까지의 cost는 알고 있으므로 다른 노드에서 계산해서 공유해준 결과를 가지고 z까지 가는 최단 경로를 찾는다. (decentralized & distributed)

초기에 각 노드는 자기와 인접한 라우터의 link와 cost만을 알고 있다.
그 다음 인접한 노드들에게 distance vector를 공유한다.
그럼 예를들어 x노드의 경우 (전달 받은 정보를 가지고 B-F알고리즘으로) y, z로 가는 least cost path를 계산할 수 있다.
일부 완성된 distance vector를 또 모든 노드들에게 공유하고 나면 모두가 완성된 최단경로를 알게 된다.
즉 정리하면
1. detect node local link cost change
2. update routing info, recalculates distance vector
3. if DV changes, notify neighbors
이다.
내 연결된 노드의 cost가 달라지거나 이웃으로 부터 바뀐 distance vector를 전달 받으면 다시 cost를 계산한다. (iterative)
변화가 생긴 노드만 주위로 정보를 전달하면 되고 변화를 감지한 노드만 asynchronous하게 알고리즘을 다시 수행하면 된다.

t0 : 그림처럼 cost가 변했다. 그리고 y가 그 변화를 감지하고 distance vector를 업데이트하여 이웃에게 알려준다. ("z에게 x까지 1이면 갈 수 있다"), x도 업데이트된 distance vector(z에게 "y까지 1이면 갈 수 있다.")를 notify한다.
t1 : 그럼 z는 그 정보를 받고 dz(x)를 5에서 2로 수정하고 변경 내역을 알린다.
t3 : 그럼 y는 z의 업데이트 내용을 수신한다. x, z로의 distance vector 값은 변화가 없으므로 따로 inform하지 않는다. (converged)

이번엔 좀 다른 경우를 살펴본자.
초기에 z는 dz(x) = 5라고 되어있을 것이다. 그런데 갑자기 그림처럼 cost가 변했다.
t0 : 이를 인지한 y가 distance vector를 업데이트한다. 그러나 아직 dz(x) = 5로 되어 있기 때문에 dy(x) = 6이라고 수정한다. ("z를 거치면 x로 6이면 갈 수 있겠다!") 그리고 DV를 Notify한다.
t1 : y의 DV(dy(x) = 6)를 전달받은 z는 dz(x) = 7이라고 수정한다. 그리고 DV를 이웃에게 알린다.
t2 : y는 다시 z의 DV를 전달받고 dy(x) = 8 이라고 수정한다. 그리고 DV를 이웃에게 알린다.
...
t44 : 계속해서 1씩 증가를 반복하다. 수렴한다.
이런 현상을 bad news travels fast라고 하고 전 상황을 반대로 good news travels fast라고 한다.
이런 상황을 막기위한 방법으로 poisoned reverse가 있다. z가 y에게 dz(x) = infinite라고 알려줌으로써 y가 z를 거쳐서 x로 가지 않도록 하는 것이다. 하지만 이는 완벽한 해결책은 아니다. predecessor node를 알 수 있는 작은 네트워크에서나 가능하다.
6. LS, DV comparison
message complexity
LS : n노드, E 링크 라면 O(nE) 번 메시지가 보내진다.
DV : 오직 이웃끼리만 msg를 보낸다.
메시지를 보내는 횟수는 DV가 훨씬 낮다.
speed of convergence
LS : O(n^2)이다. 물론 oscillations 상황의 경우 시간이 더 걸릴 수 있다.
DV : 직전에 살펴본 상황처럼 count-to-infinity 문제가 발생하면 수렴하는데 굉장히 많은 시간이 걸릴 수 있다.
robustness : 오류가 발생한 상황
LS : 각 노드가 알아서 자기 테이블을 계산하기 때문에 잘못된 link cost로 결과를 도출할 수 있다.
DV : 각 노드의 테이블이 이웃으로 전달되기 대문에 path cost가 잘못될 수 있다.
둘다 경우에 따라 error가 network로 전파된다.
'ComputerScience > Network' 카테고리의 다른 글
| Network Layer - 6. Control Plane (2) (0) | 2022.05.24 |
|---|---|
| Network Layer - 4. IP: Internet Protocol (2) (0) | 2022.05.16 |
| Network Layer - 3. IP: Internet Protocol (1) (0) | 2022.05.16 |
| Network Layer - 2. What's inside a router? (1) (0) | 2022.05.12 |
| Network Layer - 1. overview (0) | 2022.05.10 |



